Une
théorie
des
modèles
de René
Thom
Comment
l'utiliser en
SVT ? (en
travaux
2005-2006)
|
retour
page
d'accueil
Projet:
Modéliser
un être
vivant,
ou le
comportement
d'un groupe
d'êtres
vivants, ou un
organe, ou une
cellule...
... à
l'aide de la
théorie
générale
des
modèles
de René
Thom
|
|
|
Voici
quelques
pistes de
compréhension
de la
théorie
des
modèles
de René
Thom. J'assume
les
incompréhensions
et
inexactitudes
mais je serai
reconnaissant
qu'on me les signale.
Une source
principale,
l'intégrale
des
œuvres
de Thom
publiée
sous forme
d'un CR-Rom
à
commander sur
le site de
l'IHES:
http://www.ihes.fr/
jsp/site/
Portal.jsp?
page_id=217.
|
|
Un
article
relativement
accessible:

La
théorie
des
catastrophes,
Ivar Ekeland,
La
Recherche,
n°81,
septembre
1977, volume
8, pp 745-754.
Vu la
difficulté
que j'ai eue
pour en
obtenir une
copie
je la mets
temporairement
à la
disposition
des
collègues.
|
|
Remarques
:
Le travail de
Thom est
anthropomorphique,
comme il le
revendique
lui-même,
ce qui est
à mon
avis une
constante de
toute
connaissance
humaine. On ne
peut pas lui
en faire le
reproche.
Le travail de
Thom fait
appel à
la philosophie
de
façon
claire et
ouverte
(Aristote et
Platon sont
ces
références
récurrentes).
La profondeur
des concepts
énoncés
autorise une
généralisation,
que Thom a
esquissée.
Dans ce cas,
qu'importe le
chemin suivi
si la
compréhension
est au
rendez-vous !
Je pense
personnellement
que la
philosophie
est souvent un
excellent
raccourci pour
celui qui
cherche
à
comprendre
pour vivre (je
vis de la
biologie...
à mon
niveau
d'enseignant)
et non pas
uniquement
pour augmenter
son savoir.
Thom utilise
les
mathématiques
les plus
rigoureuses
qui soient,
élémentaires
d'après
certains -
Thom est le
premier
à le
dire - mais
qui
malheureusement
rebuteront
ceux qui ont
choisi des
études
de sciences
naturelles et
pour lesquels
trop souvent
les maths ne
sont qu'une
langue
étrangère
(j'en suis
particulièrement
conscient,
n'ayant acquis
des rudiments,
vite
oubliés
faute de
pratique,
qu'en classe
préparatoire).
Après
bien des
années
de SVT, il est
logique que
j'en vienne
à
remettre en
cause les
fondements de
ma discipline.
Et c'est alors
que j'ai
découvert
d'autres
mathématiques,
pas
forcément
plus
accessibles,
mais plus
solides que
les quelques
éléments
d'une biologie
théorique
inavouée.
Les
mathématiques
sont, selon
Thom, «
le langage
théorique
universel
», et
j'espère,
pour tous, une
garantie de la
rectitude
totale
d'intention de
tout
scientifique
qui les
utilise. On
dit parfois
que les
mathématiques
sont «
neutres »
du point de
vue
éthique;
il faudrait
plutôt
dire «
vraies »
ou «
bonnes »
puisqu'il
s'agit de
finalité.
Pour ceux qui
ne comprennent
pas cette
rectitude
d'intention et
qui parfois se
réclament
d'une
nécessaire
falsifiabilité
(selon
Popper), tout
à fait
légitime
(mais mal
comprise, je
crois, car ce
n'est pas sur
un relativisme
que Popper se
fonde, mais
bien sur une
confiance
toujours
renouvelée
en l'homme),
je renvoie
à un
article de
Mariano
ARTIGAS sur
Popper
particulièrement
clair : The
Ethical Roots
of Karl
Popper's
Epistemology,
disponible
à
l'adresse http://www.nd.edu/Departments/Maritain/ti/artigas.htm.
Je recommande
aussi un témoignage
de Marc
Chaperon
sur l'histoire
de la
théorie
des
catastrophes :
|
|
|
|
|
1
- Un
être
vivant c'est
une forme
vivante.
idée
n°1: la
notion
intuitive de forme
géométrique
matérielle
usuelle peut
être
étendue
à tout
processus,
même du
vivant
Idée
n°2 : la géométrie
et les outils
de l'analyse
mathématique
deviennent le
langage
universel de
compréhension
du vivant
2
- la vie est
un travail
1er
principe de
cinématique
du vivant:
les
êtres
vivants sont
des formes
stables
1er
principe de
dynamique
vivante: les
systèmes
vivants sont
stables
|
|
pages
complémentaires
plus
mathématiques
|
|
éléments
mathématiques
(Attention
!
cette page
contient des
applets java
tournant avec
geogebra.jar
qui
pèse
environ 1Mo et
doit
être
téléchargé
; c'est donc
une page
longue
à
télécharger).
modèles
continus en
SVT
|
|
|
|
1
- Un
être
vivant c'est
une forme
vivante.
|
|
Idée
n°1:
la notion
intuitive de forme
géométrique
matérielle
usuelle peut
être
étendue
à tout
processus,
même du
vivant
|
|
1ère
étape:
un objet c'est
une forme,
au sens usuel,
comme figure
(matérielle)
dans l'espace
usuel à
3 dimensions
(x, y, z).
Cette forme
est
générée
par morphogenèse
et
considérée
comme stable
(dans son
être,
dans sa
substance).
|
La
morphogénèse
c'est la
genèse
d'une forme
vivante.
À
partir d'une
autre forme,
c'est la
génération
telle qu'elle
est
actuellement
décrite
pour toutes
les
espèces
vivantes
puisque l'on
rejette toute
génération
"spontanée"
d'une forme
à
partir de
rien. D'une
façon
encore plus
générale
on peut aussi
parler d'émergence
ou d'innovation
(voir
par exemple:
René
Thom,
(1992f10) L'émergence
des
structures.
Plenary
session of the
pontifical
Academy of
Sciences,
27-31 octobre
1992. In The
Emergence of
Complexity in
Mathematics,
Physics,
Chemistry, and
Biology, B.
Pullman
éd.,
Pontificae
Academiae
Scientiarum
Scripta Varia,
89, pp. 43-64.
T22/92. (19
novembre
1992).
Un être
vivant c'est
d'abord une
forme,
matérielle,
dans l'espace
courant
à 3
dimensions,
perçue
habituellement
par le sens le
plus
développé
chez l'homme:
la vision. Le
principal
caractère
d'une forme
c'est sa stabilité,
malgré
d'éventuelles
déformations;
ce qui est un
point central
de la biologie
(une aporie
fondatrice
comme dirait
Thom - ne pas
oublier que le
livre
fondateur de
Thom a pour
titre: Stabilité
structurelle
et
morphogénèse).
Cette forme
peut
être
décrite
géométriquement.
La
géométrie
est une
branche des
mathématiques
qui
étudie
les formes
dans l'espace;
c'est-à-dire
qu'elle
s'intéresse
à
l'espace de
tout un chacun
(à
trois
dimensions).
Mais les
individus sont
multiples et
les formes
beaucoup moins
nombreuses. On
peut comparer
intelligemment
des formes (et
les faire
dériver
les unes des
autres dans
une
théorie
évolutive,
ce que l'on ne
peut faire des
individus...).
Lorsque l'on
cherche
à
nommer ce qui
est stable du
point de vue
de
l'être,
malgré
les
changements,
lorsque l'on
recherche l'universel
dans les
êtres
vivants on
utilise aussi
les mots de
structure ou
encore
d'espèce
qui
désignent
aussi la forme
sous
différents
aspects.
|
|
|
Pour
ceux que la
philosophie ne
rebute pas il
s'agit de la
forme,
au
sens
d'Aristote.
L'étant
(l'être
vivant ici)
est un
composé
(dit hylémorphique)
de matière
(le
continu qui
résiste
au changement
- attention
cette
materia prima
ne
s'identifie
que
partiellement
à la
matière
des chimistes,
elle est
puissance
informe (une
matière
sans bord,
sans
discontinuité,
non
individualisée...
) alors que la
matière
chimique est
déjà
un objet
composé
de
matière
et de forme
(imaginez de
la pierre sans
limite... ou
de l'eau... le
contenant,
bords et
quantité
participent de
la forme))
et de forme
(qui est
le point
d'arrivée
du mouvement
de
génération
à
partir de la
privation de
forme). En
biologie les
formes sont
aussi les espèces
mais cette
fois au sens
classificatoire,
le genre
(pas
forcément
au sens
Linnéen)
étant
le continu.
|
|
|
|
2ème
étape:
pour rendre
compte du mouvement
et
du changement
(qui
caractérise
non pas
l'être
mais les
accidents):
évolution
de la forme
dans la
quatrième
dimension - le
temps -, on
ajoute une cinématique
et une
dynamique.
|
Le
temps forme la
quatrième
dimension de
notre espace
de vie. Il
faut donc, en
plus de la
géométrie
une cinématique
qui est la
science des
corps en
mouvement (des
corps qui
changent de
coordonnées
dans l'espace
au cours du
temps). Enfin,
comme les
formes se
déforment
avec le temps,
il faut une dynamique
qui
décrive
ces
transformations
au cours du
temps.
|
|
Le ballon de
foot est un
objet
matériel
en forme de
sphère.
Il remplace
dans cette
illustration,
une FORME
VIVANTE, moins
visuelle car
moins simple.
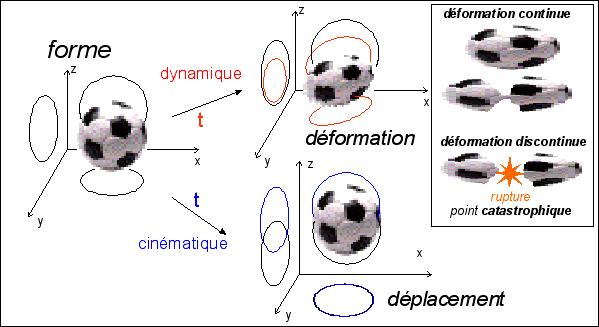
quelques
formes simples
des
êtres
vivants:
boules
(sphères)
;
bâtonnets
; filaments ;
plans (ailes)
....
mais il y a
beaucoup plus
de formes
complexes,
ramifiées,
avec des
expansions.
quelques
verbes
associés
à des
dynamiques ou
à des
cinématiques
:
s'allonger,
croître,
grandir,
diminuer,
mourir
(catastrophe),
s'accoler-s'unir
(catastrophe)
, migrer,
circuler...
|
|
|
|
3
ème
étape:
la forme, au
sens de
René
Thom, comme
figure
géométrique
d'un processus
(matériel
ou
énergétique
ou
informationnel)
dans un espace
de dimension
pouvant allant
jusqu'à
l'infini avec
une dynamique
et une
cinématique
pour
décrire
les variations
en fonctions
du temps.
|
|
|
L'idée
de Zeeman est
que l'on peut
décrire
de
façon
RIGOUREUSE
(donc)
MATHÉMATIQUE,
tous les
processus,
même du
vivant,
à
l'aide de
formes
géométriques
(si j'ai bien
compris je
crois qu'au
départ
Thom
s'était
limité
aux formes
dans l'espace
euclidien et
que c'est
Zeeman qui a
eu
l'idée
d'étendre
la
théorie).
Même si,
l'être
vivant ne peut
pas être
décrit
complètement,
à moins
de prendre un
espace de
dimension
infinie.
Dans la
pratique on
peut presque
limiter les
MODÈLES
à des
espaces de
dimension 4,
avec le temps
comme
4ème
dimension.
Le
système
vivant, dans
l'analogie
proposée
par Zeeman est
comparable
à une boîte
noire des
cybernéticiens
(un
système
dont les
mécanismes
internes ne
sont pas
accessibles).
On peut agir
sur des
paramètres
externes ou
entrées
qu'il nomme
les variables
de l'espace de
contrôle;
les
morphologies
étant
les sorties du
système.
Zeeman
n'hésite
pas à
nommer "causes"
les
entrées
et "effects"(effets
en
français)
les sorties.
Mais attention
ce n'est pas
la
causalité
au sens
philosophique
(voir page
sur les 4
causes
d'Aristote)
- cette
causalité
repose sur des
entités
qui sont
cachées
dans la
boîte
noire - mais
ce que Zeeman
appelle
"cause" c'est
l'action de
l'homme qui
perturbe le
système
vivant lors
d'une
expérience.
(Ces
paramètres
de
contrôle
sont vraiment
ceux de
l'expérience
mais la
théorie
des
modèles
peut
très
bien accepter
des
paramètres
non
opérables,
mais qui ne
feront pas ici
l'objet d'une
description).
Les
paramètres
peuvent
être
très
variés
en fonction
des processus
que l'on
désire
décrire
: par exemple
des
paramètres
comme, la
température,
le pH, la
pression, la
teneur en
dioxygène....bref,
tous les paramètres
expérimentaux
QUANTITATIFS
classiques
mais aussi des
paramètres
QUALITATIFS
(non moins
expérimentaux
(au sens du
domaine de
l'expérience
sensible)
mais dont la
description
scientifique
n'est pas
toujours
simple) comme
la forme (voir
l'exemple
ci-dessous:
passage de la
levure
Candida
albicans
d'une forme
filamenteuse (pseudomycelium)
à une
sphère
(chlamydiospore)...),
la couleur
(la couleur
d'un objet
dépend
de longueur
d'onde de la
lumière
reçue
par
l'observateur
mais la
couleur d'une
spore par
exemple
dépend
à la
fois de
paramètres
internes et
externes qu'il
est
très
difficile de
quantifier),
le
comportement
(agressivité,
passivité...)....
Un point
catastrophique
c'est un point
de
discontinuité.
L'exemple
donné
par Thom est
une image :
lorsque l'on
courbe
progressivement
une feuille de
papier et
qu'elle se
plie
brusquement;
les points du
pli forment un
ensemble
(ce que l'on
appelle un
"fermé")
de points
catastrophe
ou une
catastrophe
qui s'opposent
aux points
réguliers
(non
pliés)
de la feuille
qui forment un
"ouvert". Ce
que l'on a
appelé
la théorie
des
catastrophes
c'est un
générateur
de
modèles.
|
|
sorties
|
Boîte
noire =
système
vivant
|
la
correspondance
entrées-sorties
(= caractéristique
du
système
vivant) est
représentée
comme un nuage
de points
de l'espace
produit Rr
x Rn
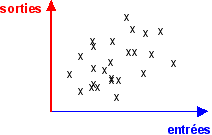
|
|
|
morphologies
ou
comportements
observés
(variables
internes)
variation
rapide
ordre local de
compréhension)
|
espace
euclidien de
dimension n :
Rn
(ouvert
de Rn)
|
|
espace
euclidien de
dimension r :
Rr
(ouvert
de Rr)
|
variables
(ou paramètres)
de
contrôle
(ou externes)
espace
de
contrôle
variation
lente
(ordre
supérieur
de
compréhension
où les
variations
sont en
quelque sorte
moyennées)
|
entrées
|
|
|
La
fonction
vivante (lien
entre les
entrées
et les
sorties) est
considérée
par le
mathématicien
comme un cas
d'application
(simplifiée
pour pouvoir
être
étudiée
géométriquement
JUSQU'À
RETOMBER SUR
DES FONCTIONS
ANALYTIQUES);
Le
système
vivant est
considéré
notamment
comme un potentiel*
qui tend
toujours
à se
stabiliser
à une
valeur
minimale (c'est
une
hypothèse
de robustesse
ou de
stabilité
que l'on
retrouve dans
tous les
systèmes
naturels).
Les potentiels
sont alors
décrits
mathématiquement
à
l'aide de
conflits d'attracteurs**.
Le
graphe
ci-dessus,
caractéristique
du
système
vivant, est
donc
considéré
comme le
«lieu
des minima
d'un potentiel
V(x,y...,u,v...)».
|
|
*un
potentiel
c'est une
fonction qui
décrit
une
capacité
en puissance
dans un espace
(champ de
potentiel)...
**
un attracteur
généralise
celle de point
d'équilibre
stable (i.e.
attractif).
Intuitivement,
un attracteur
A de X est un
régime
asymptotique
stable.
C'est un
ensemble
fermé,
X-invariant et
indécomposable
pour ces deux
propriétés
(i.e. minimal)
qui attire
(i.e. qui
« capture »
asympotiquement)
toutes les
trajectoires
issues des
points d'un de
ses
voisinages. Le
plus grand
voisinage de
A, B(A), ayant
cette
propriété
s'appelle le
bassin de A.
Dans les cas
simples, les
attracteurs
auront une
structure
topologique
simple (point
attractif ou
cycle
attractif),
seront en
nombre fini et
leurs bassins
seront de
« bons »
domaines (de
forme simple)
séparés
par des
séparatrices.
Mais cette
image est par
trop optimiste
car :
- les
attracteurs
peuvent
être en
nombre
infini ;
- les
bassins
peuvent
être
intriqués
les uns dans
les autres de
façon
inextricable;
- les
attracteurs
peuvent avoir
une topologie
très
compliquée
(attracteurs
dits
« étranges »).
(EU article
forme - Jean
Petitot)
La
théorie
des
catastrophes
élémentaires
permet de
représenter
l'ensemble
des
discontinuités
(catastrophes)
du
système
dans les cas
les plus
simples
(fonctions
lisses
à
variables
réelles)
sur
l'espace-temps
R4.
Ces
discontinuités
sont
rapportées
à des
bifurcations
(disjonction
ou
réunion)
d'attracteurs.
|
|
|
>>>éléments
mathématiques
sur la TC (page
complémentaire)
....
pour des
explications
un peu plus
détaillées
et des
constructions
élémentaires
du niveau des
classes de
1èreS
et Terminale
S.
Attention
!
elle contient
des applets
java tournant
avec geogebra.jar
qui
pèse
environ 1Mo et
doit
être
téléchargé
(c'est donc
une page
longue
à
télécharger).
|
|
«
Moyennant une
hypothèse
de
caractère
général,
la « convention
de Maxwell »
(qui exprime
en quelque
sorte
l'égalité
des « potentiels
locaux »
relatifs
à
chaque
attracteur**
de part et
d'autre de la
séparatrice)
il est
possible de
montrer que
ces surfaces
séparatrices
ne
présentent
qu'un petit
nombre de
singularités
stables,
toujours les
mêmes
(ceci,
à tout
le moins, dans
le cas
où la
dynamique
locale est une
dynamique de
gradient X
= grad V). En
ce cas, j'ai
dressé
la liste
complète
de ces
singularités,
qui sont
autant de
« catastrophes
élémentaires
» sur
l'espace-temps
R4.
En effet, ces
singularités
apparaissent
lorsque la
dynamique
locale X =
grad V est
elle-même
dans une
situation
«
critique
», par
exemple
lorsqu'un
attracteur A
est
détruit,
ou se divise
en plusieurs
attracteurs
(phénomène
que Henri
Poincaré
a
appelé
la «
bifurcation
»). On
peut faire le
tableau de
toutes les
singularités
du potentiel V
qui se
présentent
de
manière
structurellement
stable sur R4,
et donner le
modèle
algébrique
correspondant
des surfaces
de
catastrophe.
À titre
indicatif, en
voici la liste
:
- (i).
Le pli.
Destruction
d'un
attracteur, et
capture par un
attracteur de
potentiel
moindre.
- (ii).
La
fronce.
Bifurcation
d'un
attracteur en
deux
attracteurs
disjoints.
Ceci engendre
en
Hydrodynamique
ce qu'on
appelle la
catastrophe de
Riemann-
Hugoniot
(formation
d'une onde de
choc à
bord libre).
- (iii).
La queue
d'aronde.
Une surface
« front
d'onde »
se creuse en
un sillon dont
le fond est le
bord d'une
onde de choc.
Le blastopore
dans la
gastrulation
des Amphibiens
en fournit un
exemple
probable en
Embryologie.
- (iv).
Le « papillon
». Cette
singularité
du
sixième
ordre en V se
traduit par
l'exfoliation,
le «
cloquage
» d'une
onde de choc
à bord
libre.
- (v).
L'ombilic
hyperbolique.
Il s'agit de
la
singularité
présentée
par le
crêt
d'une vague
sur le point
de
déferler.
- (vi).
L'ombilic
elliptique
ou le «
poil ».
Cette
singularité
se
présente
comme
l'extrémité
d'un «
piquant
», sorte
de pyramide
effilée
à base
triangulaire.
- (vii).
L'ombilic
parabolique.
Transition
entre ombilic
elliptique et
hyperbolique ;
il se
manifeste sous
la forme en
champignon
fréquemment
présentée
par un jet qui
brise.
Ces
trois
dernières
singularités
sont
associées
à des
singularités
du potentiel V
d'un type plus
compliqué
(point de
« corang
» deux)
; elles
dirigent, en
Hydrodynamique,
la morphologie
du
déferlement
; en Biologie,
très
vraisemblablement,
elles dirigent
l'organogenèse
des processus
de capture
(phagocytose
chez les
Unicellulaires)
et de la
sexualité
(formation et
émission
des
gamètes).(in
Une
théorie
dynamique de
la
morphogenèse,
1966,
René
Thom,
1966f1.pdf,
Article
édité
in Towards
a theoretical
Biology I,
1966, C.
H.Waddington
editor., Univ.
of Edimburgh
Press,
éditeur,
p. 152-179.
Réédité
in
Modèles
Mathématiques
de la
Morphogenèse
(MMM1), 1974,
p. 252-288,
comme chapitre
12.
Réédité
in MMM2, 1980,
p. 9-35, comme
chapitre 1 )»
|
|
Remarque
*V.
I. Arnold et
son
école
ont
montré
que la
classification
des
singularités
suivant la
« modalité »
(ou nombre de
modules)
présente
une
étonnante
richesse de
structure: par
exemple, les
singularités
sans module
(dites
singularités
simples) sont
associées
aux groupes de
Coxeter An,
Dn, E6, E7,
E8, et donc
aux solides
platoniciens
(Arnold, Critical
Points of
Smooth
Functions)
(in EU, 2004,
Singularités
des fonctions
différentiables
- La
théorie
mathématique
des
singularités
et ses
applications).
Pour des
développements
ultérieurs
de la TC, je
suis bien en
peine de
fournir des
références.
Si certains
osent faire le
reproche
à
René
Thom d'avoir
été
un peu court
en
mathématiques
(voir
ci-dessous),
il n'en reste
pas moins
qu'il est non
seulement
l'inventeur de
la
théorie
mais un
merveilleux
vulgarisateur;
il manque
actuellement
(2005) en
France un
travail d'un
mathématicien
qui s'attache
à
vulgariser les
nouveaux
développements
mathématiques
de la TC...
pour les
biologistes.
(extrait de
1997i.pdf, un
inédit
que l'on
trouve sur le
CD-Rom des
œuvres
complètes):
c'est Thom qui
parle...
« En
mathématique
pure, mes
propres
résultats
n'allèrent
guère
au-delà
de
développements
limités
de certaines
singularités
de potentiel.
Il fallut la
pertinence de
mathématiciens
américains
(Milnor) ou
européens
(théorie
du
déploiement
universel,
Grauert, J.
Martinet) pour
sortir la
théorie
de son marasme
initial. Mon
seul apport
à la
théorie
mathématique
fut
d'introduire
la notion de
«
déploiement
universel
» -
corrigé
peu
après
en versel par
les
collègues
algébristes
(Mather). Il
n'y a pas de
doute que des
mathématiciens
américains
(Mather,Milnor),
puis
soviétiques
(Arnold) ont
apporté
à la
théorie
des
singularités
des
progrès
décisifs.
La vision de
ces
mathématiciens
m'a fait
comprendre
combien la
théorie
des
singularités
a des origines
profondes en
mathématiques.
C'est la
rencontre de
mathématiciens
soviétiques
comme Arnold
(souvent
férocement
critique de
mes
procédés
rustres) qui
m'a fait
comprendre
à quel
point la
théorie
des
singularités
tire son
origine de
structures
profondes
(Polynômes
de Dynkin,
carquois de
Gabriel,
théorie
des tresses,
immeubles de
Tits).
L'intérêt
de la T.C. est
bien d'avoir
attiré
l'attention
sur ces
théories
«
profondes
» dont
la source
reste (pour
moi) bien
mystérieuse.»
|
|
*
une singularité
est un
lieu où
il se passe
quelque chose
de
différent
d'ailleurs
** un germe
de fonction
réelle
en un point x
est une classe
d'équivalence
de fonctions
réelles
définies
en x, pour la
relation qui
consiste
à
confondre deux
fonctions
lorsqu'elles
coïncident
dans un
voisinage de
x.
*** un déploiement
est une
famille de
fonctions
réelles
de n variables
d'état
(x,y....)
dépendant
de r
paramètres
de
contrôle
(u, v, w,
t....).
« Le
déploiement
universel est
tout
simplement une
manière
de «
déployer
» toute
l'information
intrinsèque
renfermée
en une
singularité
»
(René
Thom,
Paraboles et
catastrophes,
p 21).
**** le potentiel
F est un germe
de fonction de
Rn
x Rr
-> R issu
d'un
déploiement
d'un germe de
fonction de Rn
-> R.
|
|
in
stabilite.pdf
p 406 -
Appendice 2
|
nom
des
singularités*
|
centre
organisateur
ou germe**
|
déploiement***
universel
(potentiel****
standard)
|
|
minimum
simple
|
V
= x2
|
V
= x2
|
|
le
pli
|
V
= x3
|
V
= x3
+ ux
|
|
la
fronce
(catastrophe
de
Riemann-Hugoniot)
|
V
= x4
|
V
= x4
+ ux2
+ vx
|
|
la
queue d'aronde
|
V
= x5
|
V
= x5
+ ux3
+ vx2
+ wx
|
|
le
papillon
|
V
= x6
|
V
= x5
+ ux4
+ vx3
+ wx2
+ tx
|
|
l'ombilic
hyperbolique
|
V
= x3
+ y3
|
V
= x3
+ y3
+ wxy
- ux -
vy
|
|
l'ombilic
elliptique
|
V
= x3
- 3 xy2
|
V
= x3
- 3 xy2
+ w(x2
+ y2)
- ux -
vy
|
|
l'ombilic
parabolique
|
V
= x2y
+ y4
|
V
= x2y
+y4
+ wx2
+ ty2
- ux -
vy
|
|
Une
classification
des potentiels
V standard
contenus dans
la boîte
noire
(grise ici)
avec
x1
= x et x2
= y, p1
=u, p2
=v, p3
=w, p4
=t
|
|
n
variables
internes ~
sorties
|
x
|
V
= x3
+p1
x
le
pli
|
V
= x4
+ p1 x2
+ p2
x
la
fronce (A)
|
V
= x4
+ p1 x2
+ p2
x + p3
la
fronce
(B)
|
V
= x5
+ p1 x4
+ p2
x3
+ p3
x2
+ p4
x
le
papillon
|
|
V
= x5
+ p1 x3
+ p2
x2
+ p3
x
la
queue d'aronde
|
|
x,
y
|
|
V
= x3
+ y3
+ p3 xy
- p1 x
- p2
y
l'ombilic
hyperbolique
|
V
= x2y
+y4
+ p3 x2
+ p4
y2
- p1 x
- p2
y
l'ombilic
parabolique
|
|
V
= x3
- 3 xy2
+ p3 (x2
+ y2)
- p1 x
- p2
y
l'ombilic
elliptique
|
|
espace
produit
Rn
x Rr
1≤
n ≤2, r
≤ 4
|
p1
|
p1,
p2
|
p1,
p2,
p3
|
p1,
p2,
p3,
p4
|
r
paramètres
externes
(modifiables
par
l'expérimentateur
ou mesurables;
tous les
autres
étant
supposés
constants)
=
paramètres
de
contrôle
~
entrées
|
|
|
Les
7 catastrophes
élémentaires
(du pli
à
l'ombilic
parabolique)
sont
expliquées
de
façon
pédagogique
avec des
applets Java
sur la page de
Lucien
Dujardin (http://perso.wanadoo.fr/l.d.v.dujardin/index.html)
Pour des
exemples, on
peut se
référer
au livre de
Christopher
Zeeman, non
traduit en
français:
Catastrophe
theory,
selected
papers.
Addison-Wesley
publishing
company,
London, 1977
et
désormais
introuvable
à
l'achat (150
euros en
occasion !!!!)
mais il y a
probablement
de nouveaux
développements
(Arnold
par
exemple...).
Pour un
aperçu
des
utilisations
de la
théorie
des
catastrophes
dans quelques
domaines des
sciences
expérimentales
on peut
notamment
consulter la
page de Lucien
Dujardin (http://perso.wanadoo.fr/l.d.v.dujardin/index.html)
Pour
une approche
accessible
à tous,
voici un
exemple
lumineux et
original par
Lucien
Dujardin et
extrait de http://pharmaweb.univ-lille2.fr/
apache2-default/labos/
parasitologie/
anglais/
Candida.html
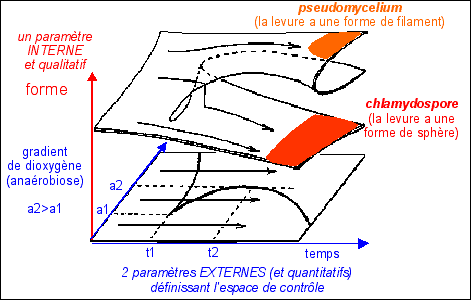
Le
modèle:
le
changement de
forme
pseudomycelium
<=>
chlamydospore
est
modélisé
dans un espace
à 3
dimensions: la
morphologie
est un
paramètre
INTERNE
(qualitatif -
il peut
exister des
formes
intermédiaires
-) et les deux
autres
dimensions
(temps et
gradient
d'anaérobiose)
sont des
paramètres
EXTERNES
(quantitatifs
et très
classiques)
qui forment l'espace
de
contrôle.
|
|
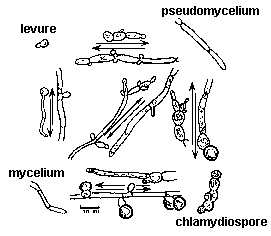
Candida
albicans est
un
unicellulaire
eucaryote
à
paroi. Il peut
se
présenter
sous plusieurs
morphologies
toutes
pourvues d'une
paroi (voir:
http://pharmaweb.univ-lille2.fr/
apache2-default/
labos/parasitologie/
images/ca1.gif
).
La forme
levure est la
plus classique
et
voisine de
celle de Saccharomyces
cerevisiae
bien connue
des
enseignants
(mais bien peu
savent que
cette levure
forme aussi un
amas ou thalle
filamenteux,
par
bourgeonnement
rapide, les
cellules
restant
accrochées
les unes aux
autres par
leur paroi).
La forme en
filament
cloisonné
(hyphe,
mot grec
signifiant
"tissu" -
par opposition
aux filaments
cœnocytiques
non
cloisonnés
nommés"
siphons"; il
semble que
certains
appellent
hyphe tout
filament...)
donnant un mycelium
(masse
enchevêtrée
de filaments
pouvant
être
très
dense comme on
peut le voir
dans un
"champignon"
au sens
courant qui
est le
carpophore ou
appareil
reproducteur
de l'organisme
mycélien)
le rapproche
des
mycètes
pluricellulaires
(on classait
cette levure
dans les
Ascomycètes
imparfaits
puisque sa
phase à
méïospore
était
inconnue... je
ne sais pas ce
qu'il en est
actuellement).
Je ne sais pas
ce recouvre le
terme
pseudomycelium
employé
ci-contre.
La forme spore
est une forme
unicellulaire
à paroi
épaissie
et à
métabolisme
réduit.
Les chlamydospore
(du grec chlamyda
= chemise)
sont
enveloppées
avant leur
libération
dans un
épaississement
du
mycélium
avec une
épaisse
paroi. Elles
sont
haploïdes.
C'est
un hôte
habituel des
muqueuses et
des
cavités
du milieu
extérieur
internalisé
(tube
digestif,
cavités
génitales...).
Elle est
habituellement
symbiote
saprophyte (se
nourrit des
déchets
cellulaires)
mais peut
devenir
parasite
(candidose
dont le muguet
des
nourrissons)
en se
développant
à
l'intérieur
des tissus
(voir ancien
cours
d'immunologie).
Quelques
observations
concernant les
culture de
Candida
albicans
- tous
les
paramètres
de
contrôle
sont
reliés
les uns aux
autres
- les
chlamydospores
apparaissent
soudainement
dans les
cultures
- les
délai
de formation
des
chlamydospores
est
relié
aux autres
paramètres
de culture:
densité
d'ensemencement
des levures ou
anaérobiose
par exemple.
«
La production
des
chlamydospores
semble
être un
phénomène
qui
obéit
à la
loi du tout ou
rien et fort
compliqué
notamment
parce que
plusieurs
paramètres
de
contrôle
jouant en
même
temps. De plus
ils doivent
franchir un
seuil et ce
seuil est
multidimensionnel.
Cette
étape
de la
morphogenèse
de Candida
albicans relie
donc des
changements
continus dans
l'environnement
à un
brusque
changement de
forme. Or la
théorie
des
catastrophes
propose un
support pour
décrire
un tel
phénomène.
»
|
|
Remarques:
* Cette
troisième
étape a
conduit
à un
succès
très
important de
ce que Zeeman
a
appelé
la
Théorie
des
Catastrophes.
Des critiques
venues d'outre
atlantique
sont alors
arrivées
ce qui a
conduit Thom,
en les
acceptant
partiellement,
à
définir
une
véritable
théorie
de l'analogie
dont quelques
éléments
sont
présentés
en annexe
ci-dessous.
* La
Théorie
des
Catastrophes
n'est pas un modèle
global qui
rendrait
compte de
l'ultime
réalité
des choses
mais bien un
méthode
d'élaboration
de modèles
locaux. La
topologie a
cela de
passionnant
qu'elle
étend
facilement par
la
pensée
son objet et
qu'il est
facile de
passer de
l'infiniment
petit à
l'infiniment
grand. Le
travail de
Jean-Pierre
Luminet (voir
par exemple L'univers
est-il infini
?, Jean-Pierre
Luminet, Les
dossiers de La
Recherche
n°21,
novembre 2005,
pp 86-89) sur
un univers
non euclidien
chiffonné
fini est
évidemment
très
attirant pour
quelqu'un qui
s'efforce,
à la
suite de
René
Thom, «
de
libérer
son [notre]
intuition du
maniement des
corps solides
dans l'espace
euclidien
à trois
dimensions R3
au profit de
schémas
dynamiques
beaucoup plus
généraux»
(SSM, p 38).
René
Thom se
méfiait
de ce projet:
«
Mais on ne
peut
espérer
a priori
intégrer
tous ces
modèles
locaux en une
structure
globale ; s'il
était
effectivement
possible
d'intégrer
tous ces
schémas
locaux en une
immense
synthèse,
l'homme serait
fondé
à dire
qu'il
connaît
la nature
ultime de la
réalité,
puisqu'il
n'existerait
pas d'autre
modèle
global
meilleur que
celui-là
; je crois,
personnellement,
que c'est
là une
exorbitante
prétention;
très
vraisemblablement,
l'ère
des grandes
synthèses
cosmiques
s'est
définitivement
close avec la
relativité
générale
et il est bien
douteux (et
sans doute peu
utile) qu'on
tente de la
rouvrir.
»
(SSM, p 39)
Mais il n'est
pas interdit
de rêver
et de penser
que cet
univers
chiffonné
pourrait
être
bien utile
pour expliquer
les
invariances
d'échelle
dans le
vivant. Et il
serait
certainement
bien plus
facile de
trouver une
vérification
expérimentale
à ces
modèles
à
l'échelle
du vivant
qu'à
l'échelle
de l'univers.
|
|
plan
Idée
n°2 :
la
géométrie
et les outils
de l'analyse
mathématique
deviennent le
langage
universel de
compréhension
du vivant
|
|
Pour
comprendre le
vivant dans ce
sens et
l'enseigner
aux
élèves
il est
nécessaire
d'approfondir
les bases
scolaires de
mathématiques
des
enseignants de
SVT et de
favoriser les
liens avec les
collègues
mathématiciens.
J'y travaille
d'arrache
pied.
On peut sans
aucun doute
s'appuyer sur
le travail
déjà
très
développé
par et/ou pour
les
physiciens.
|
|
>>>
Modèles
continus en
SVT
(page
complémentaire
donnant des
définitions
et des
explications
sur le continu
en SVT).)
Le
générateur
de
modèles
catastrophiques
permet de
réintroduire
du
continu
en SVT
alors
que la
compréhension
des
mécanismes
biologiques
fait appel
habituellement
à des
modèles
discontinus au
sens de
discrets
|
|
plan
|
|
2
- la vie est
un travail
|
|
|
En
reprenant
cette
formulation
qui m'est
chère
(voir Qu'eest-ce
que la vie ?),
je ne pense
pas que cela
nuise à
la
compréhension
de
l'œuvre
de René
Thom.
Le travail du
vivant c'est
celui de la
cinématique
des formes
vivantes et de
la dynamique
des fonctions.
Les
résultats
de la
physique, et
notamment la
définition
des travaux
virtuels en
mécanique,
peuvent
être ici
analogiquement
éclairants.
En physique
l'énergie
mécanique
est une
capacité
de travail,
produit d'une
force par un
déplacement.
Elle est
présente
sous deux
formes:
potentielle et
cinétique.
En
mécanique
analytique,
dans l'espace
de
configuration,
les travaux
virtuels sont
le produit des
forces de
liaison
(internes) et
des forces
appliquées
(externes) par
le
déplacement
infinitésimal.
Les forces du
vivant ce sont
les fonctions
(voir
un essai
d'utilisation
dans le cours
de seconde).
Le travail du
vivant est
donc
analogiquement
le produit des
fonctions
(internes et
externes) par
le
déplacement
infinitésimal
(soit autonome
soit
expérimental).
On peut
alors
énoncer
deux principes
(que Thom a
appliqué
à
toutes les
formes
naturelles
mais que je
limite aux
formes
vivantes dans
cette
présentation).
Thom
ramène
parfois ces
principes
à une
seule aporie
fondatrice
de
stabilité:
Expliquer la
stabilité
de la forme
spatiale des
êtres
vivants et ce,
en
dépit
du «
turn-over
»
constant des
molécules
qui les
constituent.
L'origine de
la vie est un
autre aspect
de cette
aporie
(in
Thèmes
de Holton et
apories
fondatrices,
1982, 5. In Logos
et
Théorie
des
catastrophes,
Colloque de
Cerisy, 7-18
septembre
1982, Jean
Petitot
(éd.),
Genève,
éditions
Patiño,
1989, pp.
285-295.
Réédité
in AL, pp.
468-481, 1982f5.pdf,
p 12)
:
1er
principe de
cinématique
du vivant
les
êtres
vivants sont
des formes
stables
(corollaire,
sauf sur
l'ensemble des
catastrophes,
où on
observe une
morphogénèse)
1er
principe de
dynamique
vivante:
les
systèmes
vivants sont
stables
(corollaire:
sauf sur
l'ensemble des
catastrophes
où on
observe une
morphogénèse);
|
|
Remarque:
un
système
est dit stable
si son
apparence
phénoménologique
ne varie pas
pour une
déformation
assez petite.
|
|
«
Tout comme
Cuvier -
à ce
qu'on dit -
reconstituait
le squelette
complet d'un
fossile
à
partir d'un
seul os, le
mathématicien
peut
reconstituer
une fonction
analytique
à
partir de ses
valeurs au
voisinage d'un
seul point
(son «
germe »
en ce point) -
par le
processus dit
du prolongement
analytique*.
En un certain
sens, toute
fonction
analytique a
la
propriété
structurale de
pouvoir se
régénérer
à
partir d'un
fragment
»
(René
Thom,
1992f10.pdf, p
4).
Les fonctions
du vivant
peuvent, dans
un
modèle
"thomien" aux
hypothèses
clairement
énoncées,
être
étudiées
par
prolongement
analytique.
Je
me suis
efforcé
d'utiliser
cette
formulation
dans le cours
de seconde de
physiologie de
l'effort
et elle est en
cours
d'élaboration
dans le cours
de
première
S sur la
glycémie.
La
relation
nutritive avec
le milieu
(source de
matière
et
d'énergie)
est une voie
vers un second
principe On
distingue
ainsi
essentiellement
deux
types
trophiques
(voir cours de
seconde): les
allotrophes
(qui
consomment les
autres, proies
vivantes ou
mortes) et les
autotrophes
(qui se
nourrissent
seuls en
capturant la
lumière
et des
matières
minérales).
Thom
écrit
que se faisant
les organismes
s'identifient
à leur
proie. (à
suivre)
|
|
plan
|
|
Annexe:
qu'est-ce
qu'un
modèle
?
|
Le
livre majeur
de René
Thom sur les
modèles
est Stabilité
Structurelle
et
Morphogénèse,
qui contient
nombre
d'intuitions
qu'il
développera
ultérieurement.
Ce livre date
de 1968 (mais
publié
en anglais en
1972 et en
français
en 1975) et
porte en
second titre:
Essai
d'une
théorie
générale
des
modèles.
«
...nous nous
trouvons face
à une
situation
présentant
un caractère
surprenant pour
l'observateur,
du fait
qu'elle
évolue
d'une
manière
imprévisible,
il y a quelque
chose
d'aléatoire
ou
d'apparemment
indéterminé
ou des
facteurs
agissant d'une
manière
non locale -
actions
à
distance par
exemple. On
essaye donc de
dominer ces
situations
à
l'aide de la
modélisation,
c'est-à-dire
en construisant
un
système
matériel
- ou mental-
qui simule la
situation
naturelle du
départ,
à
travers une
certaine analogie.
A ce point on
formule une question
sur la
situation
naturelle et,
à
travers
l'analogie, on
la
transfère
sur le
modèle
que l'on fait
évoluer
de
manière
à en
obtenir une réponse
» (Paraboles
et
Catastrophes,
1983,
Flammarion,
p125-126).
«
Supposons
qu'un
être (ou
une situation)
extérieur(e)
(X)
présente
un
comportement
énigmatique,
et que nous
nous posions
à son
sujet une (ou
plusieurs)
question(s) (
ˆQ). Pour
répondre
à cette
question, on
va s'efforcer
de
«modéliser
» (X) ;
c'est-à-dire,
on va
construire un
objet
(réel
ou abstrait)
(M),
considéré
comme l'image,
l'analogue de
(X) : (M) sera
dit le
«modèle
» de
(X). Le
modèle
(M) est
construit de
telle
manière
que, dans
l'analogie (A)
de (X) vers
(M), la
question (
ˆQ)
posée
sur (X) se
traduit en une
question
pertinente (Q)
sur (M) ;
autrement dit,
on peut poser
la question
(Q) au
modèle
(M) qui y
répondra
par une
évolution
naturelle
conduisant
à une
réponse
(R) : cela
s'appelle
« faire
jouer »
le
modèle
; l'analogie
(A), prise en
sens inverse,
permet alors
de
déduire
de (R) une
réponse
( ˆR)
valable pour
(X). On
comparera
alors cette
réponse
aux
données
empiriques...
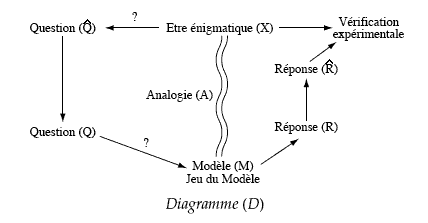
L'ensemble de
ces
opérations
est
résumé
dans le
diagramme (D)
ci-dessous
:»
|
|
texte
et figure de
R. Thom
extraits de
Modélisation
et
scientificité,
P. Delattre,
M. Thellier,
éd.,
Élaboration
et
justification
des
modèles.
Actes du
colloque, ENS,
9-14 oct.
1978. Tome 1,
Maloine-Doin,
Paris, pp21-29
(référence
du CDRom des
œuvres
complètes
de l'IHES:
1978f7.pdf
|
|
|
|
Un
modèle
est un
système
ou une loi analogique
d'un
être
réel.
|
L'analogie
désigne
la relation
ontologique
entre
l'être
réel et
le
modèle.
Mais du point
de vue
épistémologique,
l'élaboration
du
modèle
(et donc la signification
du
modèle
pour
l'observateur)
repose sur un
processus que
Thom
définit
le plus
simplement du
monde à
l'aide du
Logos: un
modèle
c'est une réponse
à une question
de l'observateur.
Faire
fonctionner un
modèle
au sens des
scientifiques,
c'est le
questionner.
C'est entendre
(voir,
toucher,
sentir,
mesurer...) la
réponse
donnée
à une
question.
|
Un
modèle
fournit
à
l'observateur
une réponse
à une question.
|
|
|
Remarque
personnelle:
on devrait
pouvoir
assimiler la question
thomienne au problème
scientifique
(ou
problématique
?), si cher
à
certains
didacticiens.
Quel
enseignant de
SVT n'a pas
été
confronté
à
l'obstination
de certains
didacticiens,
dont on
diffuse les
idées
notamment dans
les iufm,
à
présenter
les cours
à
partir d'un problème
biologique
censé
être
issu du
questionnement
de la nature
par le
naturaliste
(et donc par
l'élève
apprenti
naturaliste).
J'ai toujours
pensé
que si cette
méthode
pouvait
être
effectivement
celle du
chercheur,
elle ne
s'appliquait
que de
façon
très
impropre
à
l'élève
qui a plus
besoin de
connaissances
et de
formation aux
méthodes,
buts qui
peuvent
être
atteints de
bien d'autres
manières
que celle qui
est à
la racine de
la
méthode
scientifique
expérimentale
(voir mon
ancien site
lorsque
j'étais
à
l'iufm).
|
|
Le
modèle,
comme
système
ou loi
analogique
d'un
être
réel
(X)
observé,
est construit
contre l'aléatoire
(l'apparemment
indéterminé,
contre lequel
lutte tout
scientifique:
Thom dit que
le but de
toute science
est
d'éradiquer
l'indéterminé)
et le non
local
(c'est-à-dire
ce qui agit
à
distance, par
une induction
délocalisée
par exemple...
et Thom cite
le centriole*).
*Un
modèle
est efficace
s'il
répond
à la
question
posée.
C'est le
problème
de la justification
du
modèle.
|
Un
modèle
permet :
OU de prévoir
le
comportement
de
l'être
(X)
observé
(c'est
l'efficacité
pragmatique)
OU
de comprendre
le
comportement
de X,
même si
on ne peut pas
le
prévoir
(c'est la
justification
théorique).
|
Il est
donc faux de
dire que l'on
teste la validité
du
modèle
(ou
plutôt
sa
falsificabilité
ou encore sa
vérificabilité,
ou même
sa
scientificité
pour des
esprits plus
positivistes)
lorsque l'on
compare le
comportement
de l'objet
réel au
comportement
du
modèle.
Car la raison
d'être
du
modèle
c'est la
réponse
^R à la
question ^Q.
Le seul
comportement
vrai est celui
de
l'être
X. Pour un
modèle
quantitatif et
pour lequel la
question est
de
prévoir
le
comportement
quantitatif de
X, la
validité
est bien
sûr
réduite
à cette
prévision
mais ce n'est
pas le cas
général.
La
vérité
d'un
modèle
est dans
l'analogie.
Il n'y a pas
de
degrés,
juste des
points de vue.
Pour expliquer
cette
distinction,
Thom parle de
justification
a priori et
a
posteriori.
- La
justification
d'un
modèle
a priori est
la convenance
analogique
(le
modèle
est pertinent,
acceptable,
juste,
légitime,
adapté...);
cette
justification
fait tout
l'originalité
d'un
chercheur;
Thom parle de
pari ou
de mise.
Plus la
convenance
analogique est
forte moins le
pari est
élevé.
(On
pourrait par
exemple
classer 2
analogies
usuelles selon
un pari
croissant:
|
pari
à mise
minimale
|
pari
à mise
maximale
|
fonctionnement
local d'une
enzyme
voir
cours
1èreS
|
analogie
clé /
serrure
(forme
spatiale-fonction
locale)
|
analogie
effet
enzymatique /
morphogenèse
sur
l'espace-temps
R4
|
phase
cytoplasmique
(voir
page
sur la cellule)
|
phase
liquide
(solutions
très
concentrées)
|
phase
solide avec
propriétés
rhéologiques
thyxotropiques
|
-
La
justification
a
posteriori est
celle de
l'efficacité,
d'utilité,
c'est la
convenance
fonctionnelle.
C'est la
partie la
moins
hasardeuse,
Thom parle de
gain
(et reproche
ainsi leur
faible valeur
(et non leur
faible véracité)
aux
modèles
puisque
celle-ci est
déterminée
par le rapport
entre les
gains et le
pari. Comme le
pari est
à mise
minimale, la
valeur est
minimale ; mais
son
explication
est peu claire
car le rapport
gain/mise est
d'autant plus
faible que la
mise est
importante,
à gain
égal;
donc la mise
ce serait
plutôt
l'inverse de
ce qu'il
appelle
justification
a priori :
plus un
modèle
est
justifié
moins la mise
est
importante;
c'est donc le
rapport
Justification
a priori/Justification
a
posteriori
qui varie dans
le sens
recherché).
<---
Voir texte
ci-contre.
Le
danger
étant
que l'on fasse
jouer le
modèle
sans question
clairement
énoncée.
Comme dans
l'apprentissage
de la
démarche
expérimentale,
à quoi
peut-il servir
de faire une
expérience
sans
hypothèse
à
tester ? Faire
jouer un
modèle
pour
répondre
à des
questions que
l'on ne se
pose pas c'est
comme utiliser
un outil pour
d'autres
usages que
celui pour
lequel il a
été
conçu
(ce n'est pas
un
enrichissement
c'est un
détournement,
et ici une
perte de
signification).
Chaque
modèle
a son propre
niveau
d'abstraction
et doit
répondre
à une
question
précise.
Remarque:
On peut
pousser cette
règle
assez loin et
chercher
à en
comprendre
l'origine. Il
est
habituellement
illégitime
d'utiliser un
modèle
établi
à un
certain niveau
de
réalité
(comme par
exemple
à un
niveau
moléculaire)
pour essayer
de le faire
jouer à
un autre
niveau (comme
par exemple
à un
niveau
organique
embryonnaire
pour la mise
en place des
organes...).
Thom oppose
l'ontologie
verticale
entre les
niveaux
d'abstraction
et la
localité
du
modèle
et « suggère
qu'on
retrouvera un
niveau plus
pertinent
d'ontologie en
pratiquant une
théorie
horizontale
des niveaux
d'organisation».
Il conclut en
disant:
«il
est
universellement
vrai que la
syntaxe
engendre
l'ontologie et
pas seulement
au niveau du
code
génétique».
|
|
«...
dans la mesure
où
l'expérimentation
coûte
cher, on doit
faire appel
à des
modèles
très
bien
justifiés
a priori.
Mais toute
modélisation
est un pari.
Il y a une
mise et un
gain : la mise
c'est la
justification
a priori,
le gain celle
a
posteriori.
Or, dans la
science
moderne, les
choses se
passent
exactement
dans le sens
contraire : la
justification
a posteriori
est
pratiquement
négligeable
par rapport
à celle
a priori. Puisque
l'on veut
faire des
expérimentations
coûteuses,
la machine
expérimentale
doit
fonctionner
à tout
prix. Selon
moi, c'est
là
justement une
des
principales
causes de la
stérilité
de la science
moderne,
stérilité
entendue comme
carence de
conceptions
théoriques
générales.»
(Paraboles
et
Catastrophes,
1983,
Flammarion,
p101)
«...la
justification
« a
posteriori
» du
modèle
: elle
résulte
de la
comparaison
entre la
réponse
(ˆR) du
modèle
et la
donnée
empirique ; si
la
réponse
(ˆR) est
conforme
à
l'expérience,
le
modèle
en sera
validé
« a
posteriori
». Dans
la mesure
où
l'analogie (A)
entre (X) et
(M)
apparaît
comme peu ou
mal
fondée,
il n'en sera
que plus
surprenant si
le
modèle
donne des
réponses
satisfaisantes
; en un
certain sens,
tout acte de
modélisation
est un pari,
où le
parieur joue
du
modèle.
Le
caractère
fécond
du
modèle
apparaît
essentiellement
dans le
rapport
(Justification
a
posteriori)/(Justification
a priori)
(C'est le
rapport
Gain/Mise du
pari). De ce
point de vue,
les
modèles
de la Science
moderne, qui
sont en
général
très
fortement
justifiés
a priori (personne
n'ose plus
parier), ont
de ce fait
même un
rendement
très
faible...»
(Modélisation
et
scientificité,
P. Delattre,
M. Thellier,
éd.,
Élaboration
et
justification
des
modèles.
Actes du
colloque, ENS,
9-14 oct.
1978. Tome 1,
Maloine-Doin,
Paris, pp 4)
|
|
|
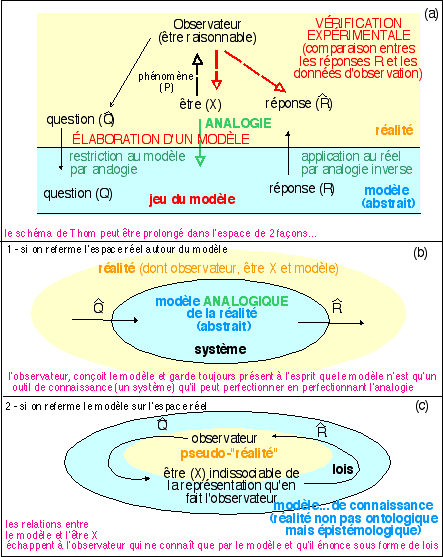
Je
ne suis pas
sûr
d'avoir
compris mais
voici une
illustration
(b) de ce qui
me semble
pouvoir
refléter
la
pensée
de Thom (a) et
qui la met en
opposition (c)
avec des
idéalistes
(au sens de
non
réalistes),
ce qui peut
par exemple
être le
cas de
matérialistes,
pour qui le
modèle
est en fait
seule
réalité
de
connaissance
puisque
l'être X
ne peut
être
connu que par
l'homme et sa
connaissance
est
inséparable
de
l'être
de celui qui
connaît
et de la
connaissance
elle-même.
On remarquera
que selon
l'évolution
(b) on a
tendance
à
parler de
modèle
ou de
système
(ce qui va de
pair avec un
certain
réalisme)
alors qu'en
(c), le terme
de lois est
plus
approprié
(les lois sont
bien des
modèles
analogiques
des
phénomènes
observés),
terme qui
s'accommode
bien d'un
certain
idéalisme.
|
|
|
La
deuxième
partie de
l'intervention
de Thom est
basée
sur la
recherche
d'une analogie
qu'il qualifie
d'ontologique
et qui est
basée
sur le
modèle
de
système
de type
boîte
noire (type b
de mon
schéma)
qu'il emprunte
si je ne me
trompe
à
Zeeman puisque
c'est lui qui
à
partir de SSM
a eu
l'idée
d'appliquer
les principes
des
modèles
catastrophistes
aux
systèmes
cybernétiques
de type
"boîte
noire" dont on
ne
connaît
que les
entrées
et les sorties
(voir La TC,
Science ou
Philosophie,
1989f9, in La
Recherche...
manquant, p
6).
Son propos
est, à
partir des
systèmes
de type
boîte
noire, de
justifier dans
le cadre de la
TC les
modèles
présentés
la très
forte analogie
que l'on peut
atteindre par
la
méthode
proposée.
C'est une
véritable
ontologie
mathématique
qu'il veut
démontrer,
dans le cadre
de l'exemple
proposé.
|
|
plan
|
|
Notes
*
Les centrioles
sont
constitués
en paires de
cylindres
courts de 9
triplets de
microtubules
(associés
par des
protéines)
disposés
perpendiculairement
l'un à
l'autre et
occupant le
centre du
centrosome
(chez de
nombreux
eucaryotes
à
l'exception
notable des
plantes) qui
se duplique en
même
temps que
commence la
replication de
l'ADN (phase S
du cycle
cellulaire).
Le centriole
fils est
généré
par
auto-assemblage
des composants
protéiques
sur un
côté
du centriole
père,
perpendiculairement
à ce
dernier. Les
deux
centrioles
d'une paire ne
sont pas
identiques de
par leur
position mais
aussi de par
leur
morphologie et
leur fonction.
Chez les
vertébrés,
le centriole
fils est
souvent
capable de
générer
un cil non
mobile de
fonction
inconnue. Chez
la
Paramécie
on a
montré
que
l'orientation
des
corpuscules
basaux,
homologues des
centrioles,
déterminait
l'orientation
des
rangées
de cils et du
cytosquelette
sous-jacent.
Des greffes
(de ?) ont
permis de
modifier
l'orientation
de plusieurs
rangées
de cils qui
battent alors
dans un sens
opposé
à celui
des
rangées
bordantes, ce
qui rend
impossible le
déplacement
synchronisé
de la cellule.
Ces motifs
sont
héritables
sans
modification
entre cellules
se
reproduisant
par
reproduction
sexuée
(méïose,
échange
de noyaux et
scissiparité)
et
asexuée
(scissiparité
sans
échange
de noyaux ni
méiose)
sur plus de
100
générations.
(in Biologie
moléculaire
de la cellule,
Alberts et
al., 1995,
Flammarion,
819 et s.)
retour
texte
|
|
René
Thom,
exposé
donné
à
l'Inspection
Académique
de Toulon, 20
mai 1992, in
CDRom
œuvres
complètes
1992i.pdf)
(c'est moi qui
souligne)
«
Au
début
du XVII.
siècle,
les travaux
des
mathématiciens
italiens
(résolution
de
l'équation
du
troisième
degré)
introduisent
la notion de
polynômes.
Stevin et
Viète
conçoivent
pour la
première
fois un nombre
réel
comme un
nombre
décimal
illimité.
De là
résulte
l'écriture
d'une loi
physique comme
une fonction y
= f (x),
permettant
ainsi la
formulation
d'un
déterminisme
strict.
Galilée,
en comparant
le mouvement
de la pierre z
lancée
vers le haut,
qui monte et
redescend,
trouve la
même
équation
Z = z° -
1/2 gt2.
Le mouvement
forcé
d'Aristote ne
se distingue
pas du
mouvement
naturel. Le
mouvement tire
son
unité
de
l'individualité
de la fonction
polynôme.
L'être
physique est
défini
par la forme
mathématique...
Deux
siècles
plus tard, on
définira
les fonctions
analytiques,
fonctions qui,
dotées
d'un
développement
de Taylor
convergent,
déterminent
leur valeur en
tout point
dès
qu'on en
connaît
le germe
autour d'un
point via le
procédé
du «
prolongement
analytique
». Il
n'est pas
exagéré
de
prétendre
que la
prédiction
quantitative
des «
Sciences dures
» est
toute
entière
fondée
sur l'emploi
du
prolongement
analytique.
En un certain
sens, le
procédé
galiléen
a permis la récupération
de l'accident
qui
arrêtait
la
prédiction
«
naturelle
» de la
physique
aristotélicienne.
Ce
procédé
a donné
d'admirables
preuves de sa
puissance,
surtout au
XIX.
siècle,
pendant lequel
s'est
développé
tout
l'outillage
des fonctions
analytiques.
Mais le
domaine du
réel
où joue
«
l'exactitude
déraisonnable
des lois
physiques
» -
selon la belle
expression
d'E. Wigner -
n'en demeure
pas moins
conceptuellement
étroit,
car elle
repose en
dernière
analyse sur
des
symétries
d'ampleur
cosmique
postulées
sur la
structure
globale de
l'espace
temps.
Déjà
la
Mécanique
Quantique
avait
renoncé
au
déterminisme
au profit
d'une
interprétation
statistique :
la Physique
des hautes
énergies
n'est rien de
plus qu'une
récupération
de l'accident
de plus en
plus
poussée,
vers des temps
de plus en
plus brefs (10-33cm).
Dans la
hiérarchie
Comtiste des
Sciences :
Mathématique,
Physique,
Chimie,
Biologie, il
est bien connu
que les
dernières
de ces
sciences, la
Biologie
surtout, sont
rebelles
à la
mathématisation.
Mais
dès
1890,
l'impossibilité
de
résoudre
le
problème
des trois
corps avait
conduit Henri
Poincaré
à
développer
la «
Dynamique
Qualitative
»,
où l'on
se
préoccupe
moins de
calculer les
solutions que
de
déterminer
l'allure
globale de
l'ensemble des
trajectoires
d'un
mouvement. En
1903, Hadamard
met en
évidence
dans un
système
déterministe,
le
phénomène
de «
dépendance
sensible des
conditions
initiales
» pour
le flot
géodésique
d'une surface
à
courbure
totale
négative.
Duhem montre
dans sa
«
Théorie
Physique
» (1906)
que ce
phénomène
ruine toute
possibilité
de
prédiction
à long
terme, bien
que le
système
soit
analytique. Ce
fait fut
redécouvert
en 1980
grâce
à
l'emploi des
ordinateurs,
et aux
développements
ultérieurs
de la
Dynamique
théorique
(Smale,
Kolmogorov,
Sinai... etc).
Aujourd'hui,
on
espère
du «
chaos »
une
interprétation
des
phénomènes
à
topologie
complexe
observés
dans les
fluides, les
transitions de
phase de la
matière
condensée,
la physiologie
des
organismes...
etc.
Il est
probablement
prématuré
de tirer des
conclusions
sur cette
entreprise de
domestiquer
l'indescriptible.
Pour des
raisons
théoriques,
toutefois, on
se rend compte
que
l'hypothèse
des gradients
mise en avant
par la
théorie
des
Catastrophes
en 1970
n'était
pas sans
motivation
sérieuse.
Car dans un
système
gradient
analytique,
la
prédictibilité
est possible,
même
à long
terme, et de
plus, la
théorie
des
bifurcations y
est
mathématiquement
complète.
Au contraire,
dans un
système
dynamique
général,
la notion
même
d'attracteur
exige
l'observation
du
système
en un temps
infini, ce qui
est
difficilement
réalisable
dans
l'étude
d'un
système
concret. C'est
pourquoi je
pense que
l'étude
morphologique
des formes
récurrentes
dans
l'évolution
d'un
système
est un
programme tout
à fait
raisonnable ;
et la
considération
des
successions de
ces motifs
peut
être
discrétisée
et soumise
à une
analyse
initialement
statistique,
et
ultérieurement
déterministe.
Après
tout la
Météorologie
qu'on
prétend
«
chaotique
» ne
procède
pas autrement.
Et dans
l'examen des
interactions
entre motifs,
régimes
stables
locaux, on
devrait voir
réapparaître
les
caractéristiques
conflictuelles
qui sont
celles de la
théorie
des
catastrophes...
C'est du moins
l'idée
que -
très
personnellement
- je soumets
à votre
réflexion.
»
retour
texte
|
|
|
|
plan
|
![]()





