|
|
|
|
|
|
Avertissements: |
||||||||||||||||||||||||||||||
|
Nota Bene Dans le modèle de la boîte noire (voir page principale) qui va rester en toile de fond dans cette page, ne pas oublier que les variables internes inaccessibles sont des paramètres de sortie notés x et y et que les paramètres d'entrée externes et contrôlables sont notés u, v, w et t ou encore a, b, c et d. Ce qui diffère un peu de l'habituelle utilisation de y=f(x) et demande un peu d'attention. Nous utiliserons la lettre F et non la lettre V pour désigner le potentiel, comme dans l'article d'Ivar Ekeland. De façon inhabituelle, F(x) ne désigne pas le résultat observé mais c'est x qui est le résultat, la fonction reste cachée et F n'en est qu'un modèle. Pour "voir" le comportement du système il ne faut pas "regarder" les F(x) mais les x seulement. Les surfaces (qui donnent leur nom à la catastrophe) ou les courbes (projections ou ensemble de bifurcations) représentant les points singuliers de F (points catastrophiques) nous permettent de visualiser les différentes valeurs critiques de x en fonction des paramètres de contrôle (on approche ainsi ce que l'on appelle la structure de l'attracteur (ou des attracteurs): figure mathématique qui explique la stabilité de la fonction). Il ne faut donc pas confondre la forme du potentiel (qui approche la fonction cachée) et la forme de l'attracteur (ou des attracteurs en conflit) qui est représentée par l'ensemble des catastrophes. |
|
* Attention ! les applets sont normalement appelées directement lors du chargement de la page (qui télécharge alors geogebra.jar - environ 1Mo). Sinon rendez-vous sur le site de http://www.geogebra.at/cms/. *le
contenu de
cette page
(repris
principalement
de Paraboles
et
catastrophes,
p54s)
s'adresse
à des
collègues
de SVT et
à des
élèves
de
lycée
(de classes
préparatoires
ou des
premières
années
d'université);
il est
rédigé
par un
professeur de
SVT et n'est
pas
destiné
à des
mathématiciens. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
1. De
la fonction au
potentiel
standard |
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
1. De la fonction au potentiel standard |
||||||||||||||||||||||||||||||||||
|
Exemples
(d'après
Paraboles et
catastrophes,
p54s): |
|
La stabilité d'une fonction en un point (ou au voisinage d'un point) est définie intuitivement comme la capacité de cette fonction à revenir à ce point après une petite perturbation. On utilisera ici la notation F pour désigner un potentiel qui est un germe de fonction définie de RnxRr vers R , C∞ à l'origine O et qui constitue un germe h de fonction de Rn en R, C∞ à l'origine O. Ce qui signifie que F dépend des variables internes x1,...xn et des paramètres externes de contrôle u1,...ur avec F( x1,...xn ; 0,... 0)= h ( x1,...xn). Le déploiement universel étant la famille de fonctions réelles des n variables internes x, dépendant de r paramètres u. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
Rechargez la page html pour réinitialiser l'applet. |
|
|
|
De façon analogue, toujours pour n = 1, la fonction (le germe) h (x) = x4 perturbée par un terme ux2 donne un minimum pour u > 0 et un maximum (relatif) et deux minima (relatifs) pour u < 0. Pour augmenter les perturbations déplacez (en la sélectionnant) la courbe f(x) dans l'applet ci-dessous. Vous pouvez ainsi supprimer un minimum et le maximum pour u < 0. Enfin vous pouvez ajouter un autre terme de perturbation en vx en sélectionnant la formule de f(x) qui apparaît alors dans une fenêtre de saisie (saisissez par exemple "+ 0.5 x" ou "-0.5 x" puis ENTER et la courbe modifiée s'affiche (attention au point, les espaces n'intervenant pas) pour rester dans le domaine des petites perturbations). Ainsi le déploiement x4+ux2 présentant pour u < 0 deux minima et un maximum est moins stable que le déploiement x4+ux2+vx qui n'a qu'un minimum. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
Si l'on augmente ainsi l'exposant k de xk la fonction devient compliquée et peu stable (tapez par exemple x5 - 0.5 x3 -0.5 x à la place de x4 dans l'applet précédente ; attention les puissances demandent de saisir d'abord la touche "^" puis "touche espace" puis "le chiffre de puissance"; la fonction g(x) modifiée présente alors deux minima et deux maxima, même s'ils sont peu nets à cette échelle - pour changer d'échelle il vous faut le programme complet geogebra qui n'est vraiment pas long à télécharger). On privilégie alors les déploiements « stables », à savoir, pour le dire intuitivement, qui résistent à de petites perturbations. Ainsi le déploiement universel ou potentiel standard pour x3 est x3+ux et pour x4, x4+ux2+vx (voir le tableau ci-dessous). |
|
|
|||||||||||||||||||||||||||||||||
|
|
(1)
une singularité
est un
lieu où
il se passe
quelquechose
de
différent
d'ailleurs |
||||||||||||||||||||||||||||||||||
|
a et b sont modifiables en sélectionnant le point à gauche au niveau de chaque paramètre et en utilisant les touches + et - du clavier pour modifier leur valeur. |
|
Remarque: vous pouvez dans Geogebra (complet), tracer automatiquement la dérivée, les tangentes, déterminer les extrêma.... et tant d'autres fonctionnalités précieuses. |
|
On peut tracer ces potentiels standard dans geogebra et voir leurs variations. On entre d'abord de petites valeurs des paramètres externes (0.5 par exemple) en objets libres, puis la formule du potentiel, en objet dépendant. Ensuite, en sélectionnant le point à gauche au niveau de chaque paramètre, vous pourrez modifier sa valeur à l'aide des touches + et - de votre pavé numérique...(mais vous ne pourrez plus modifier la fonction). Vous pouvez aussi rentrez une formule générale avec tous les paramètres que vous pourrez fixer à 0 pour obtenir toutes les courbes. Pour les courbes en 3D (n=2) il faut utiliser une autre logiciel (j'utilise gnuplot). Voici un exemple d'utilisation de Geogebra pour la fronce. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
|
2. Exemple: l'ensemble des points critiques associé au potentiel standard F = x4 + ux2 + vx |
|||||||||||||||||||||||||||||||||
|
Gnuplot
est LE
PROGRAMME
GRAPHIQUE 2D
ET 3D GRATUIT
que j'ai
utilisé.
Gnuplot est
un fichier
exécutable
UNIX que l'on
peut trouver
facilement sur
le net
(travaillant
sous Mac OS X
j'ai
utilisé
Gnuplot 4.0.0
( http://gnuplot.sourceforge.net)
avec le
terminal
graphique
AquaTerm (http://aquaterm.sourceforge.net)
(la
bibliothèque
X11 (qui se
trouve sur le
disque
d'installation
OSX mais n'est
pas
installée
par
défaut)
devant aussi
être
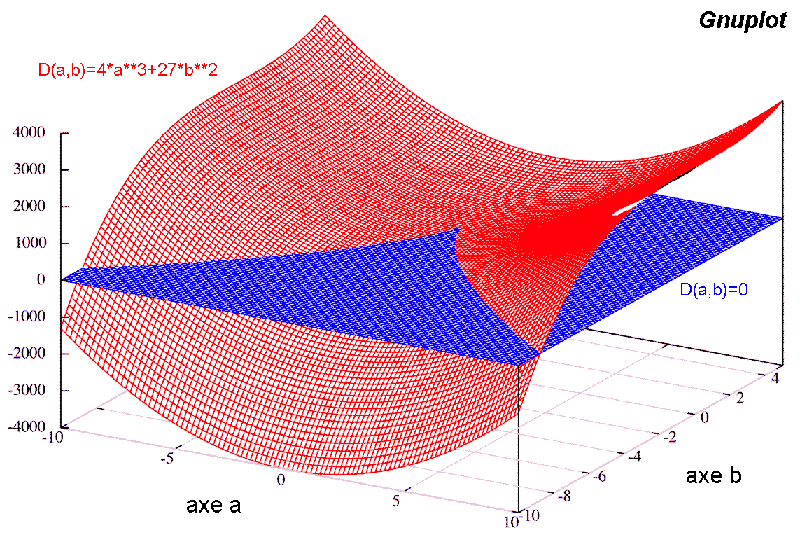
installée). Commandes tapées sous Gnuplot pour obtenir le graphe ci-dessous: (gnuplot> set hidden3d gnuplot> set ticslevel 0 gnuplot> set isosamples 100, 100 gnuplot> set grid gnuplot> set yrange [-10:5] gnuplot> splot f(x,y)=4*y**3+27*x**2, f(x,y), z=0, z ) |
|
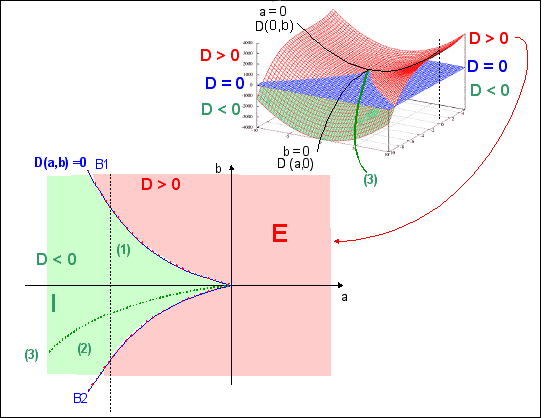
Pour étudier un potentiel standard on cherche les points critiques pour lesquels la dérivée première s'annule, c'est-à-dire où le potentiel standard F présente un MINIMUM STABLE OU NON. Utilisons à nouveau le potentiel standard associé à la catastrophe fronce: F = x4 + ux2 + vx. L'ensemble des points critiques est donc formé par les racines de l'équation dF/dx = 0. C'est une équation algébrique du troisième degré 4x3+2ux+v = 0 ou x3+ ax+b = 0 (avec a=u/2 et b=v/4) qui possède au moins une racine réelle et au plus trois racines réelles selon la valeur du discriminant D (D=4a3+27b2). Si D < 0, il y a trois racines réelles distinctes, pour D > 0, il n'y a qu'une racine réelle (et deux complexes conjuguées) et pour D = 0, il y a trois racines réelles mais certaines coïncident (pour D = 0 et a ≠ 0 ou b ≠ 0, deux racines réelles sont égales et pour D = 0 et a = b = 0, les racines sont toutes trois égales). Le
graphe
correspondant
à
l'équation
D(a,b)=0 dans
le plan (a,b)
est
appelé
"ensemble
de bifurcation"
de F. C'est
l'ensemble des
points (du
plan (a,b))
où les
"choses
changent";
là
où la
stabilité
de F
"bifurque" en
présentant
un ou deux ou
trois points
de
stabilité:
ce sont des
points de conflit
entre régimes
stables
reliées
mathématiquement
à des attracteurs
(chaque
minimum
stable, est
relié
à un
attracteur).
L'ensemble des
points de
catastrophe
est
défini
qualitativement
par l'ensemble
des points de
conflit entre
attracteurs. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
Donc on peut résumer les caractéristiques du potentiel standard correspondant à la catastrophe fronce déduites de l'étude de ses points critiques par ce tableau: |
|
B
est une parabole
semi-cubique
(définie
par D(a,b)=0)
dans le plan
de
contrôle
(a,b). Le plan (a, b)0 passant par D=0 comprend deux régions correspondant à deux domaines de D(a,b): - E, en rouge dans (a,b)0 pour des valeurs positives de D, et - I, en vert dans (a, b)0 pour des valeurs négatives de D. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
Si on complète le schéma précédant avec les potentiels F (dans les cercles) associés à chacun des domaines de la courbe D dans le plan (a,b) on obtient une vue plus claire de la signification des racines de dF/dx=0 (points rouge et point rose avec une barre horizontale). |
|
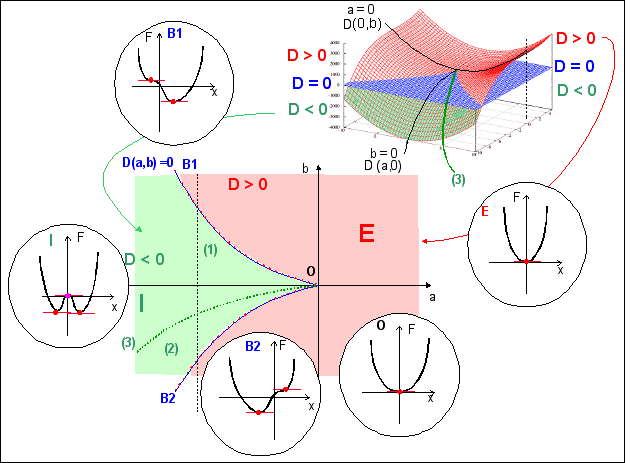 Ensemble de bifurcation de F (équation D(a,b)=0) et sections particulières de F(x,u,v) (cercles) où x prend des valeurs critiques (u =2a et v =4b) |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Lorsque plusieurs minima existent (reliés à plusieurs attracteurs comme en I, B1, B2), y-a-t-il des critères qui permettent de savoir quelle position est privilégiée et donc la PLUS STABLE ? Deux
conventions
existent pour
résoudre
cette
incertitude:
la convention
de Maxwell et
la convention
de retard. |
|||||||||||||||||||||||||||||||||
|
* convention ou règle de Maxwell, arbitraire mais simple Le point stable sera donc celui de potentiel minimal, par exemple c1 si F( c1) < F( c2), dans le cas de deux racines c1 et c2 (domaine I). |
|
La dénomination convention de Maxwell par René Thom vient de l'utilisation d'une règle similaire par Maxwell pour lever l'indétermination en v (volume) de l'équation de Van der Waals: F(p, v)=0 dans l'intervalle de pression (p) où l'on a trois racines réelles en v, ce qui décrit un mélange de phases gazeuses et liquides. |
|
Cette
convention
conduit
à
considérer
uniquement
deux cas
où un
point peut
être
catastrophique
(attention
catastrophique
ne veut dire
ni instable ni
stable, mais
c'est un point
où "il
se passe
quelque chose
de discontinu
sur le fond
continu...
lorsque l'on
fait
légèrement
varier (on
perturbe) les
paramètres
externes"): |
|||||||||||||||||||||||||||||||
|
|
Une excellente analogie est celle du modèle mécanique (une bille dans une forme dont la section verticale est celle de F ou encore un modèle hydraulique -comme celui présenté par Ivar Ekeland). Dans le cas de la convention de Maxwell on considère que la bille se situe toujours au point le plus bas (potentiel minimal). Il y a donc bien sûr une incertitude qui n'est pas levée dans le cas où les deux minima sont strictement égaux. On voit encore ici que la connaissance de l'état du système (causalité au sens scientifique d'une causalité efficiente, contenue dans le modèle) ne permet pas de prévoir le comportement du système (indéterminisme). |
|
|||||||||||||||||||||||||||||||||
|
Vous pouvez voir le code de l'applet: cata3mx.java |
|
Voici une applet (modifiée) de Lucien Dujardin (http://perso.wanadoo.fr/l.d.v.dujardin/index.html) qui présente un modèle qui obéit à la règle de Maxwell: c'est le minimum le plus bas qui est toujours choisi et il y a une incertitude lorsque deux minima sont égaux (cette incertitude n'est pas prise en compte dans le modèle qui choisit l'une des deux racines pour représenter la couleur (morphologie) de sortie). Les trois racines de x3+ ax+b = 0 sont représentées par des traits verticaux rouge et le minimum est représenté par un trait horizontal rouge.
|
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
* règle du retard ou du délai parfait (delay law) Lorsque qu'un minimum est atteint cette valeur est conservée tant que ce minimum est stable, même si un autre minimum existe, qu'il soit de potentiel inférieur ou égal ou supérieur.
|
|
On notera que cette convention conduit à présenter le système comme ayant une mémoire puisque la morphologie de sortie (donc le minimum choisi du potentiel) dépend du chemin suivi pour l'atteindre. Selon le chemin suivi dans l'espace de contrôle (en u,v) on obtient donc des morphologies (x) différentes pour des mêmes valeurs des paramètres u et v (ce que vous pouvez tester par l'applet ci-contre). |
|
Pour l'analogie mécanique (une bille dans une forme dont la section verticale est celle de F ou encore un modèle hydraulique -comme celui présenté par Ivar Ekeland) et dans le cas de la règle du retard, on considère que la bille se situe toujours au premier point stable atteint (sans inertie). La bille ne peut changer de place que si le minimum devient instable et qu'elle peut alors tomber dans un minimum situé plus bas. Il n'y a jamais d'incertitude de position de la bille. Cette convention conduit à ne considérer qu'un seul cas où un point peut être catastrophique (attention catastrophique ne veut dire ni instable ni stable, mais c'est un point où "il se passe quelque chose de discontinu sur le fond continu... lorsque l'on fait légèrement varier (on perturbe) les paramètres externes"): le minimum de potentiel cesse d'être stable: x est un point de bifurcation. |
|||||||||||||||||||||||||||||||
|
Voici une applet (modifiée) de Lucien Dujardin (http://perso.wanadoo.fr/l.d.v.dujardin/index.html) qui présente un modèle qui obéit à la règle du retard: lorsque deux minima peuvent être atteints ce n'est pas celui qui est le plus petit qui est choisi mais le premier atteint selon le chemin suivi. Les trois racines ne sont pas représentées ici, seule la racine choisie grâce à la règle du retard est représentée d'un trait vertical de couleur dont la couleur représente la morphologie de sortie du système.
|
|||||||||||||||||||||||||||||||||||
|
Vous pouvez voir le code de l'applet: cata3rd.java |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
La catastrophe élémentaire associée au potentiel standard F = x4 + ux2 + vx est la fronce (cusp en anglais) car l'ensemble des points catastrophiques dessine une fronce: elle obéit à l'équation dF/dx = 0 c'est-à-dire à l'équation algébrique du troisième degré 4x3+2ux+v = 0 ou x3+ ax+b = 0 (avec a=u/2 et b=v/4). |
|
Les
lignes de
commande
tapées
dans Gnuplot
pour obtenir
la surface
ci-contre (y=p1
et z=p2)
sont: On peut fortement améliorer la représentation... |
|||||||||||||||||||||||||||||||||
|
|
|
une fronce (cusp) dans l'espace (x, a, b) dessinée par l'ensemble des points de catastrophe de la catastrophe élémentaire associée au potentiel standard F = x4 + ux2 + vx
|
|
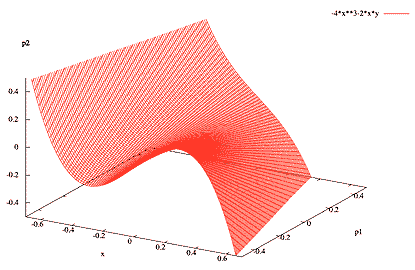 courbe tracée avec gnuplot (voir ci-contre) : x et p1 (= 2a = u) sont les axes horizontaux et p2 (= 4b = v) est l'axe vertical |
|||||||||||||||||||||||||||||||
|
|
|
Tracé dans Grapher de la surface avec x, u et v appartenant à [-1,5; 1,5] L'application Grapher est contenue dans le système Mac OS 10.4 et permet de tracer d'innombrables courbes en 2D et 3D et les visionner dans l'espace très facilement. Cette image exportée n'est pas un fichier grapher et ne peut donc êre manipulée dans l'espace. |
|

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
3. Extension à la structure des attracteurs ou des ensembles de bifurcation définissant les 7 catastrophes élémentaires |
|||||||||||||||||||||||||||||||||
|
|
Avertissement: |
|
On
représente
les
attracteurs
dans ce que
l'on appelle
l'espace
des phases
(voir
définition
dans page
complémentaire
sur les
modèles
continus en
SVT).
On peut aussi
représenter
la caractéristique
du
système
dans l'espace
des
morphologies
que l'on peut
aussi appeller
espace des
dynamiques
(u,v..., x,
y...). On ne
peut
représenter
facilement que
des espaces de
dimension 2 ou
plus
difficilement
3. Pour la
dimension 4,
on utilise des
sections. Dans
un espace de
dimension ≤
3 l'attracteur
a la forme
d'un point,
d'une droite,
d'une courbe
[x=f(u)],
éventuellement
fermée,
ou d'une
surface [x=f(u,v)].
(f
désigne
ici la
fonction
représentée
par le
potentiel F ou
V). |
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||
|
0 |
|
Soit une "dynamique" représentée par un potentiel V d'équation
Cette dynamique n'est pas comptabilisée dans les catastrophes élémentaires car un système naturel qui lui obéit est dépourvu de toute dynamique contrôlable. La cinétique associée peut être celle d'un oscillateur harmonique non amorti (voir page sur le continu, 3.2 b). |
|
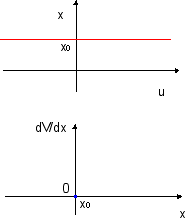 forme de l'attracteur dans l'espace des phases |
|
Dans l'espace (x ,u) , la dynamique est représentée par une droite d'unique ordonnée x0 (équation x(u)=x0). u est un paramètre inopérant. Si u est le temps, la morphologie (x) est constante. Il n'y a qu'un seul attracteur, c'est le plus simple (et le plus radical) qui soit: un attracteur ponctuel (fixe) (en bleu) dans l'espace des phases (x , dV/dx). |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
1 |
|
La première catastrophe correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel quadratique : dV(x,u)/dx
= 3x2+u Cette dynamique est associée à des cinétiques développées par des oscillateurs harmoniques non amortis (voir page sur le continu, 3.2 a). Elle
ne semble pas
vraiment
présente
dans les
systèmes
vivants, avec
un attracteur
aussi stable.
Pour
être
perçu
comme stable
le
système
devrait
être
conservatif
(sans
"frottement"
ou perte
d'énergie).
Or l'on pense
que la plupart
des
systèmes
métaboliques
sont
dissipatifs.
Mais ce point
de vue
pourrait
changer. |
|
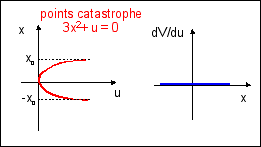 forme de l'attracteur dans l'espace des phases |
|
Dans l'espace des dynamiques (x,u), le potentiel est représenté par un pli. L'attracteur unique prend la forme d'une droite (ensemble de bifurcation) dans l'espace (x,dV/du). |
|||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2 |
|
La deuxième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel quadratique : cette fois u et v sont des paramètres opérant sur la forme du potentiel. Cette dynamique est associée à des cinétiques développées par des oscillateurs harmoniques amortis (voir page sur le continu, 3.2 b). Je me suis efforcé de présenter ce système dynamique dans la synthèse des protéines avec la spirale polysomiale (voir cours de 1èreS, la fonction enzymatique, partie 3.2 ). Il y a fort à parier que ce système dynamique est un des plus courants dans les dynamiques "cycliques" de la cellule. |
|
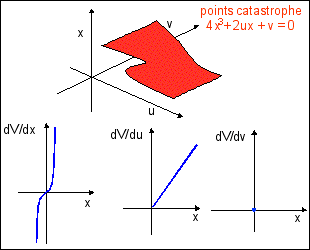 forme de l'attracteur dans l'espace des phases |
|
Dans l'espace des dynamiques (x,u,v), le potentiel est représenté par une fronce. Deux attracteurs s'affrontent (voir partie 2 ci-dessus). L'ensemble de bifurcation est une parabole semi-cubique dans le plan de contrôle (u,v,0) dans l'espace des dynamiques (voir ci-dessus). |
|||||||||||||||||||||||||||||
|
|
|
Variante: |
|||||||||||||||||||||||||||||||||
|
3 |
|
La troisième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel de la forme : u, v et w sont des paramètres opérant sur la forme du potentiel. w modifie la pente de la tangente au centre de gravité. Pour visualiser la forme du potentiel utilisez Geogebra ci-dessous par exemple. Les
points
critiques
où
|
|
La
forme de la
surface des
points
critiques
associés
au potentiel V(x,u,
v, w) est
déduite
progressivement
des sections
faites pour
u=constante: 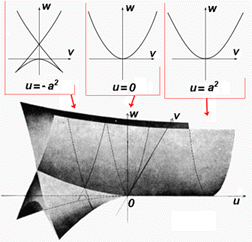 in Thom, stabilité, p 104 |
|||||||||||||||||||||||||||||||
|
|
|
« Une surface « front d'onde » se creuse en un sillon dont le fond est le bord d'une onde de choc. Le blastopore dans la gastrulation des Amphibiens en fournit un exemple probable en Embryologie. »(1966f1 p7). |
|
||||||||||||||||||||||||||||||||
|
|
|
« Examinons maintenant s'il peut exister des conflits de régime au voisinage d'une telle singularité; il faut pour cela que l'équation présente quatre racines réelles (sinon, on ne pourrait obtenir deux minima pour V). Il faudra donc se placer à l'intérieur du triangle curviligne de la queue d'aronde pour u<0. Comme l'un des rebroussements de ce triangle définit une catastrophe de Riemann-Hugoniot, on aura dans ce triangle une onde de choc, ligne de conflit entre les deux régimes qui, partant du rebroussement, aboutit en un point du côté opposé. C'est là,comme il est aisé de s'en convaincre, la seule possibilité topologique pour le partage des régimes. Si l'on suit la variation des sections lorsque u décroît, on peut ainsi décrire qualitativement la queue d'aronde. Pour u>0, on a une courbe-pli qui sépare un régime stable du régime vide (pas d'attracteurs); pour u=0, cette courbe présente à l'origine un point de courbure infinie et pour u négatif, il en sort deux rebroussements limitant un triangle curviligne en queue d'aronde. Il apparaît, à l'intérieur du triangle deux régimes séparés par une courbe joignant un des rebroussements au point double ou en un point pli, si on adopte la convention de Maxwell. La queue d'aronde a été depuis longtemps répertoriée en géométrie algébrique ; mais je ne pense pas que sa signification comme singularité stable des fronts d'onde, ait été clairement reconnue jusqu'à présent. On la trouve en Physique, dans la théorie des fronts d'onde dans les plasmas [9] et on l'a redécouverte tout récemment comme singularité des surfaces de Landau associées à certains diagrammes de Feynman. On peut d'ailleurs la réaliser assez facilement en optique géométrique classique comme singularité de caustiques. En embryologie, on proposera au chapitre 9 de considérer les extrémités du sillon blastoporique comme des queues d'aronde. » (in Stabilité, p 104-105) |
|||||||||||||||||||||||||||||||||
|
4 |
|
La quatrième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel de la forme : u, v, w et t sont des paramètres opérant sur la forme du potentiel. Pour visualiser la forme du potentiel utilisez Geogebra ci-dessous par exemple. |
|
|
|
le papillon |
|||||||||||||||||||||||||||||
|
|
|
Les trois dernières catastrophes sont de corang 2 (admettent deux variables internes) et sont associées à des phénomènes de déferlement, émission de gamètes et autres bourgeonnements.... |
|||||||||||||||||||||||||||||||||
|
5 |
|
La cinquième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel de la forme : u, v et w sont toujours des paramètres opérant sur la forme du potentiel. |
|
|
|
l'ombilic hyperbolique |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
6 |
|
La sixième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel de la forme : u, v et w sont toujours des paramètres opérant sur la forme du potentiel. |
|
|
l'ombilic elliptique |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
7 |
|
La septième catastrophe élémentaire correspond à une dynamique de gradient X=-grad>(V), V étant un potentiel de la forme : u, v , w et t sont toujours des paramètres opérant sur la forme du potentiel. |
|
|
l'ombilic parabolique |
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||