La théorie des catastrophes par Ivar Ekeland

LA RECHERCHE N° 81 SEPTEMBRE 1977, VOLUME 8, PAGES 745-754

Ivar Ekeland, ancien élève de l'École normale supérieure, est actuellement maître de conférences de mathématiques à l'université Paris IX Dauphine et à l'École polytechnique. Ses travaux sur la théorie des jeux et le contrôle optimal l'ont conduit à s'intéresser à la théorie des catastrophes.


Figure 1. A. Le professeur René Thom, créateur de la théorie des catastrophes. B. Le «chien de Pavlov » : un système à une variable interne, la faim du chien, et un paramètre extérieur, la hauteur du son, modélisable par une fronce. C. Charaxes jasius sortant de sa chrysalide.

La théorie des catastrophes une nouvelle conception du modèle mathématique utilisable en sciences.

La théorie des catastrophes est due à René Thom, actuellement professeur de mathématiques à l'Institut des hautes études scientifiques. Ses premiers travaux, sur des questions de géométrie, lui ont valu en 1962 la médaille Fields, la plus haute consécration pour un mathématicien. Mais dès cette époque il commençait une réflexion sur l'état actuel de la science qui, au fil des années, l'amenait à élaborer, sous le nom de théorie des catastrophes, une nouvelle conception du modèle mathématique utilisable en sciences. Cette théorie aboutissait rapidement à des résultats mathématiques nouveaux et profonds (démontrés par R. Thom lui-même, B. Malgrange, S. Smale, J. Malher). Elle jetait aussi, de manière élégante, un pont praticable vers la biologie et la linguistique. La publication en 1972 du livre de R. Thom, Stabilité structurelle et morphogenèse, marquait la pénétration de la théorie des catastrophes dans le domaine public ; à tel point qu'à l'heure actuelle elle échappe en grande partie à son auteur. C'est ainsi qu'une école dirigée par Christopher Zeeman a pris aujourd'hui un important développement. Nous adopterons ici une attitude résolument « thomiste ». Cet article est une tentative de lecture du livre de 1972, à la lumière certes des acquis récents, mais en cherchant à traduire fidèlement la pensée de l'auteur. II ne faudrait pas croire que celle-ci soit si clairement exprimée qu'elle nous rende la tâche facile.

Les animaux-machines.

Qu'est-ce qu'un être vivant ? II ne semble pas que nous soyons plus aptes à répondre à cette question primordiale que du temps de Newton. Peut-être même en sommes-nous plus loin que du temps d'Aristote. En effet, nous sommes dressés à attendre une réponse mécaniste se traduisant par des équations. C'est sans doute ce qui permet de comprendre que les enfants connaissent le système de Copernic et expliquent savamment les éclipses. Ce penchant de notre culture déteint aussi sur la biologie moderne, selon laquelle un être vivant est un système physico-chimique ouvert aux influences extérieures, constitué de N variables internes en interaction suivant N équations différentielles. Certains phénomènes vitaux peuvent être décrits par des variables macroscopiques, comme la tension artérielle ou la position du squelette. Mais d'autres se déroulent à l'échelle cellulaire, telle la propagation de l'influx nerveux dans un neurone. Les moins intéressants ne sont pas ceux qui se passent à l'échelle moléculaire, comme la duplication du DNA. Au total il existe une masse énorme de variables internes, dont chacune peut être chiffrée à un instant donné par une mesure.

Le comportement de l'être vivant est régi par un déterminisme physico-chimique. Rappelons-nous la célèbre formulation de Laplace : « Nous devons envisager l'état présent de l'univers comme l'effet de son état antérieur et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome : rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux. » (Essai philosophique sur les probabilités). De façon analogue, nous devons envisager l'état présent du système comme l'effet de l'état et du stimulus antérieurs, de même que l'état et le stimulus présents sont la cause de l'état qui va suivre. La théorie des catastrophes se sépare du déterminisme classique comme de l'indéterminisme quantique. Elle fait sienne l'idée d'un déterminisme régissant les phénomènes vitaux et s'exprimant par un système d'équations différentielles. Par contre, elle renonce à la tâche surhumaine d'identifier les N variables internes et d'expliciter les N équations. Qui, en effet, saura jamais combien il faut de données pour décrire une simple cellule ? N = 102, 104, 106 ? Et qui écrira jamais les N équations différentielles décrivant le comportement ? Et les aurait-on écrites, quels renseignements pourra-t-on jamais tirer de problèmes de cette dimension ? Un problème aussi simple que celui des trois corps, en mécanique céleste, n'implique que dix-huit équations différentielles, et pourtant ü n'est toujours pas complètement résolu. La théorie des catastrophes postule un déterminisme sous-jacent, mais accepte qu'il reste caché.

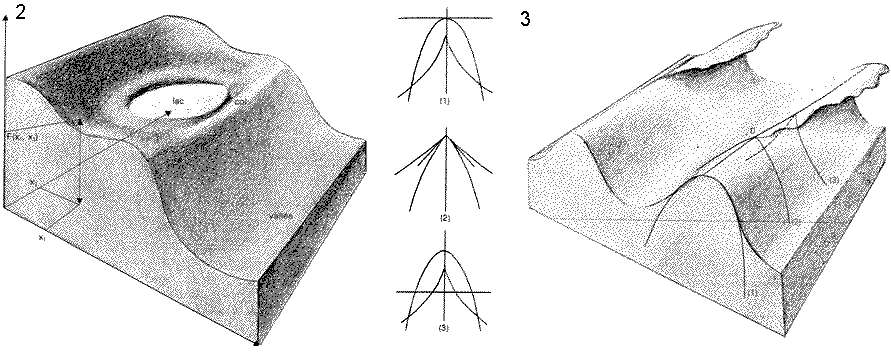
Figure 2. Le modèle hydraulique à deux dimensions.
Le graphe représente le potentiel F (p1 ..., pn). Les minimums locaux correspondent aux bassins et les maximums aux sommets d'un relief facile à imaginer : un lac retenu par un col. L'érosion sera catastrophique : lorsque le col s'effacera, l'eau se déversera dans la vallée inférieure.

Figure 3. Vague déferlante.
On croit reconnaître une catastrophe du type ombilic hyperbolique. Bien que les sections successives puissent interpréter le déferlement, point catastrophique, aucun modèle hydraulique ne peut confirmer cette explication du phénomène.

Étudier un système, c'est décrire et prévoir ses interactions possibles avec un observateur. Étudier un être vivant, ce sera donc décrire et prévoir ses réponses aux stimulus extérieurs. Le contraste entre la complexité supposée du système à étudier, le nombre quasiment infini de variables nécessaires pour le décrire, et le caractère rudimentaire des stimulus qu'on lui applique, dépendant d'un ou deux paramètres au plus, touche parfois au ridicule. Quelle commune mesure y a-t-il entre un chien affamé et un signal sonore ? Mais une expérience bien conduite aboutit à les associer en un seul système, le « chien de Pavlov », où la hauteur du son est l'unique paramètre extérieur.
Multiplicité et inaccessibilité des variables internes xl, ..., xN. Petit nombre et maniabilité des paramètres externes p1, ..., pn. Voilà les idées maîtresses de la théorie des catastrophes. Reste à savoir quel parti on peut en tirer. Pour la commodité de l'exposé, nous séparerons une théorie « restreinte » d'une théorie « généralisée », empruntant bien entendu cette terminologie à la théorie de la relativité.

La théorie des catastrophes restreinte.

La théorie des catastrophes s'intéresse à des systèmes (S) dont l'état interne est décrit par N variables internes xl, ..., xN. D'une manière générale, ces variables internes sont supposées cachées, soit en raison de leur trop grand nombre N, soit parce qu'elles sont inaccessibles à l'expérience. Par contre, les paramètres externes p1, ..., pn que l'on fait agir sur le système sont supposés en petit nombre et bien connus. De manière précise, on supposera toujours n ¾ 4. Cette restriction est justifiée par des raisons mathématiques que nous développerons plus tard. Notons qu'il ne faut pas comprendre p1, ..., pn comme l'ensemble des paramètres susceptibles d'influer sur (S) en tout état de cause, mais comme ceux auxquels on limite l'étude, les autres étant supposés constants. Dans le cas du système « chien de Pavlov », n = 1, alors que bien d'autres choses qu'un signal sonore peuvent influer sur le comportement d'un chien. La théorie des catastrophes restreinte est fondée sur l'existence d'un potentiel F (p1, ..., pn, xl, ..., xN ) régissant à lui seul le système. Physiquement, cela signifie qu'à toute valeur p1, ..., pn imposée aux paramètres externes, les variables internes xl, ..., xN répondent en se plaçant sur un minimum local de la fonction F (p1, ..., pn). Mathématiquement, c'est le seul cas où l'on saura résoudre les équations différentielles décrivant le système dxi/dt = - d F (p1, ..., pn, xl, ..., xN )/ dxi avec 1 ¾ i ¾ N.

On dit alors qu'elles dérivent d'un potentiel. Cette hypothèse ne sera vérifiée que si la « dynamique externe » réglant les paramètres est lente, et la « dynamique interne » exprimée par les équations rapide. Ainsi, les systèmes ne seront jamais hors équilibre, l'évolution sera suffisamment lente pour qu'à chaque instant on retrouve l'état d'équilibre initial. La mécanique, la physique, la chimie fournissent elles aussi des exemples de systèmes régis par un potentiel, qui est dans la plupart des cas une énergie. Nous considérons ici que le potentiel F restera tout aussi caché que les variables internes xl, ..., xN : la théorie des catastrophes restreinte postule simplement son existence sans chercher à l'expliciter.

La meilleure façon d'illustrer ce qui précède est certainement le modèle hydraulique. Plaçons-nous en dimension N = 2 (fig. 2), la dimension 1 faisant l'objet de l'encadré 1. On peut envisager deux approches possibles. Soit p1, ..., pn fixés, alors x1 et x2 deviennent tout simplement des coordonnées planes, repérant un point sur une carte, et F (p1, ..., pn, x1, x2 ) désigne l'altitude de ce point. Le potentiel F (p, ..., pn) dessinera donc une montagne, au relief arrondi pour que la fonction F (p1, ..., pn) soit bien différentiable. Les minimums locaux de la fonction F (p1, ..., pn) correspondent aux bassins, les maximums locaux aux sommets, les autres points où la pente s'annule aux cols. Les équations 1 décrivent les trajectoires des eaux de ruissellement qui finissent soutes par s'accumuler au fond des bassins. On peut concevoir qu'une partie reste en équilibre sur les sommets ou les cols, mais c'est un équilibre instable, qui traduit surtout une hésitation sur la direction vers laquelle s'écouler. Le plus léger facteur suffit à le rompre, et toute l'eau s'écoule vers un des bassins, au fond duquel elle se retrouve en équilibre stable. D'une manière générale, chaque bassin a une zone d'influence bien délimitée par une crête qui va de sommet en col, représentant une de ces lignes de partage des eaux bien connues des géographes.

Si maintenant on fait varier de façon continue les paramètres p1, ..., pn, on verra le relief se modifier progressivement, les bassins se combler, de nouveaux sommets pousser, les anciens se déplacer et disparaître, avec toute la lenteur des transformations géologiques. Le point important à observer est que cette évolution, pour régulière qu'elle soit, peut se traduire par des phénomènes soudains (du moins à l'échelle des temps géologiques) ; ainsi, quand un col ferme le bassin d'un lac de montagne (fig. 2), c'est au moment précis où le col s'effacera que le bassin disparaîtra, et que le lac se précipitera dans la vallée inférieure. II y a pour le col une altitude critique : l'abaisser au-dessous, si peu et si doucement que ce soit, déclenche un phénomène irréversible et brutal, que l'on peut à bon droit appeler catastrophe.

Mais la réponse du système à l'action des stimulus n'est pas toujours déterminée sans ambiguïté. Dans le cas simple de la dimension 1, pour les valeurs intermédiaires du stimulus p entre -8 et + 8, il y a deux équilibres stables, donc deux réponses possibles. Comme le système doit se déterminer entre l'un et l'autre (!a variable interne x doit choisir entre les deux minimums du potentiel), il faut une règle supplémentaire. Nous allons en donner deux, observées l'une et l'autre dans les systèmes naturels.

Le modèle hydraulique permet de comprendre les prémisses de la théorie des catastrophes.

1. Le modèle hydraulique à une seule dimension

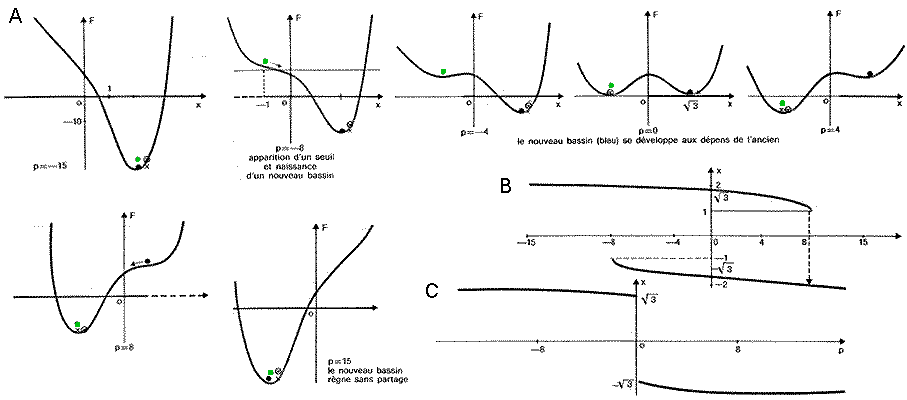
Ce modèle permet de comprendre les prémisses de la théorie des catastrophes. Le système ne comporte qu'une variable interne x et un paramètre externe p, reliés par le potentiel Fp (x) = px + (x2- 3 )2. Faisons varier p de - 15 à + 15 et examinons les déformations du potentiel Fp (fig. A). Quand p prend de grandes valeurs négatives (p < - 8), le potentiel Fp présente un seul minimum local, qui est aussi global. II y a un seul bassin, dont l'influence s'étend sur toute la droite des x. Pour p = - 8, on voit apparaître un col délimitant un nouveau bassin, qui dorénavant se développera aux dépens du premier. Tant que - 8 < p < 8, les deux bassins coexisteront, le nouveau se creusant et prenant de l'importance aux dépens du premier. Pour p = 8, le col les séparant s'efface, l'ancien bassin se vide dans le nouveau, qui subsiste seul pour p > 8. Si maintenant on repart en arrière, ramenant p de 15 à -15, on observe les mêmes phénomènes en sens inverse réapparition de l'ancien bassin, qui finit par supplanter le nouveau. On peut fabriquer une petite « machine à catastrophes » en réalisant un profil matériel qui se déforme suivant la loi indiquée, et en posant une bille dessus. On verra la bille tomber précisément quand p franchit la valeur 8 (à l'aller, bille noire) et la valeur - 8 (au retour, bille en couleur).

Cette machine à catastrophes obéit à la règle du retard. Celle-ci consiste en ce que le système reste sur un équilibre stable jusqu'à l'ultime moment où celui-ci disparaît. La figure B présente la réponse x à l'excitation p. On notera que, pour une même excitation p, le système peut se trouver dans deux états différents, le choix de l'un ou de l'autre étant déterminé par la façon dont l'excitation a été amenée à la valeur p. Si par exemple p = 0, l'état du système peut être x = - ˆ3 ou x = ˆ3 ; ce sera x = - ˆ3 si le système se déplaçait sur la branche inférieure (si par exemple l'excitation a décru régulièrement de p =-15 à p = 0), et x = ˆ3 dans le cas contraire. L'état du système dépend de la situation antérieure, il se souvient d'où il vient.

D'autres systèmes suivent la règle de Maxwell. Celle-ci consiste en ce que la variable interne se déplace à chaque instant sur un minimum global du potentiel. Nous avons matérialisé cette idée par des croix (x à l'aller, (x) (x rond) au retour). Pour - 8 < p < + 8. deux minimums locaux se croisaient exactement pour p = 0. Le saut aura donc lieu en p = 0 à l'aller comme au retour. Sur le graphique C, représentant la réponse x à l'excitation p, on notera que l'ambiguïté est levée, sauf pour p = 0. Tant que p est non nul, la règle de Maxwell suffit à déterminer l'état du système. Il n'y a plus d'effet de mémoire.

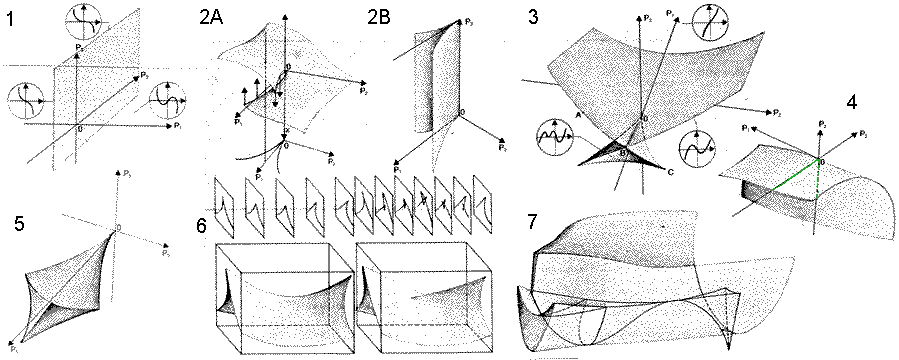
2. Les sept catastrophes élémentaires

Le théorème fondamental de la théorie des catastrophes restreinte, en dimension 3 (trois paramètres externes), énonce l'existence de cinq ensembles de catastrophes élémentaires. A chacun d'eux est associé un système décrit par un potentiel dépendant d'une [(1), (2), (3)] ou de deux variables internes [(4), (5)). L'extension à quatre paramètres implique l'introduction de deux formes nouvelles ((6), (7)). Leur représentation est beaucoup plus malaisée, car on passe en dimension 4. II est à noter que la forme de ces ensembles nous est familière, et que leurs noms sont choisis pour souligner leur ressemblance avec des objets usuels.

Remarque du copiste: les formules des potentiels semblent différer d'avec les sources habituelles; j'ai homogénéisé en attendant de vérifier les figures.

(1) Le pli associé à un potentiel de la forme Fp (x) = x3 + p1 x. Si l'on applique la règle du retard, l'ensemble de catastrophes est le plan p1 = 0. L'allure de Fp de part et d'autre de ce plan est indiquée sur la figure.

(2) La fronce : potentiel Gp (x) = x4 - p1x2 - p2x.
(2A) Fronce à deux dimensions et en appliquant la règle du retard; on a représenté sur un même dessin les valeurs (p1, p2) des paramètres et la réponse x du système.
(2 B) Fronce à trois dimensions : on complète en introduisant le troisième paramètre p3 qui est en fait inopérant.

(3) La queue d'aronde : Potentiel Hp (x) = x5 + p1x3 + p2x2 + p3x. L'allure de la fonction Hp est présentée dans chacune des trois régions délimitées par l'ensemble de catastrophes, tracé selon la règle du retard.

(4) L'ombilic hyperbolique (la vague.). Potentiel Jp (x1, x2) = x1 3 + x23 + p1x1x2 - p2x2 - p3x1. Les portions en couleur des axes p2 et p3 sont tracées sur la surface.

(5) L'ombilic elliptique (le poil) : c'est essentiellement une pointe à trois pans. Potentiel Kp (x1, x2) = x1 3/3 - x1x22 + p1(x1 2 + x22) - p2x1 - p3x2.

(6) Le papillon : potentiel Lp (x) =x6 + p1x4 + p2x3 + p3x2 + p4x.

(7) L'ombilic parabolique (le champignon) : potentiel Mp (x1, x2) = x1 2 x2+ x24 + p1 x1 2 + p2x22 - p3 x1- p4 x2.

 

« Points plis », « points fronce », « queues d'aronde », « ombilics hyperboliques ou elliptiques » sont autant d'ensembles de catastrophes.

 

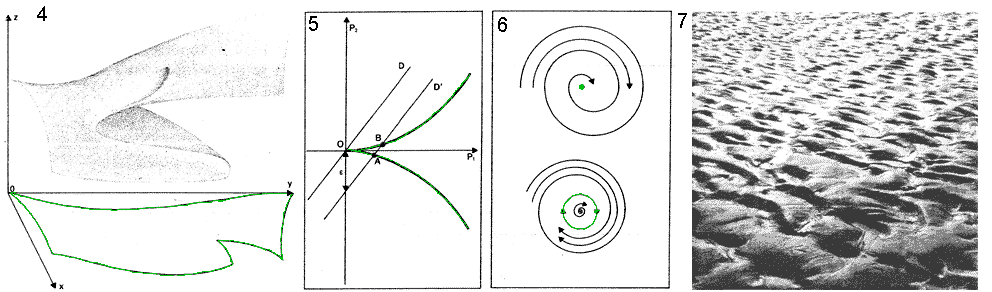
Figure 4. Le théorème de Sard. Si l'on prend une surface de l'espace à trois dimensions et qu'on la projette sur un plan (xOy), on obtient un contour apparent assez compliqué. Le théorème de Sard affirme que ce contour est de « mesure nulle », c'est-à-dire qu'il occupe peu de place. Intuitivement, on peut l'imaginer comme formé par des lignes qui n'ont pas d'épaisseur.

Figure 5. Le théorème fondamental de la théorie des catastrophes restreinte s'applique à des systèmes « généraux ». Pour faire comprendre cette expression, considérons un système à deux paramètres (p1, p2) dont l'ensemble de catastrophes est en couleur sur la figure. On en fait un système à un seul paramètre p1, en liant p2 par la relation p2 = mp1 représenté sur la figure par la droite D. Le nouveau système a l'origine comme point catastrophique. Or c'est un point fronce, et le théorème fondamental, affirmant qu'un système à un paramètre ne devrait présenter que des points plis, est en défaut. Pour le retrouver, il suffit de remplacer la relation p2 = mp1 par p2 = mp1 - e, c'est-à-dire de décaler D en D'. L'origine se dédouble alors en deux points A et 8. C'est que la droite D' est en position générale par rapport à l'ensemble en couleur, alors que la droite D occupe une position très particulière et instable.

Figure 6. On peut passer de façon continue de la figure du haut à la figure du bas, d'une dynamique ne présentant qu'un équilibre stable (en couleur) à une dynamique présentant un équilibre instable (en gris) et une orbite périodique stable (en couleur). C'est un prototype de catastrophe métabolique.

Figure 7. Formes naturelles. La puissance de la théorie des catastrophes est qu'elle peut modéliser, décrire une multitude de formes ou objets naturels. Avant qu'elle soit formulée, nous ne savions pas qu'une cloque, qu'une goutte, qu'un cil, qu'un sillon, qu'un filament... étaient des ensembles de catastrophes. (Cliché J. Gaoïtti.)

 

La règle du retard ou la règle de Maxwell lèvent l'ambiguïté.

La plupart des systèmes naturels, à commencer par le modèle hydraulique, obéissent à la règle du retard. Celle-ci consiste en ce que le système reste sur un équilibre stable jusqu'à l'ultime moment où celui-ci disparaît. Imaginons un observateur immobile, il constatera qu'un saut aura lieu pour p = 8 à l'aller et p = - 8 au retour (fig. A de l'encadré 1). Par contre, le point p = - 8 est franchi sans encombre à l'aller comme le point p = 8 au retour. Si l'on considère te graphique de la figure B, on remarque que la réponse x à l'excitation p n'est pas entièrement déterminée par le présent, elle tient compte du passé, et en ce sens on peut dire que le système considéré possède une mémoire. Si l'on fait aller et venir p entre -8 et + 8, on obtient un cycle d'hystérésis, analogue à ceux observés en magnétisme. L'état d'un système du type retard dépend donc de la situation antérieure.

D'autres systèmes suivent une règle différente : celle de Maxwell dans laquelle la variable interne se déplace à chaque instant vers un minimum global du potentiel (et non plus un minimum local). En physique, par exemple, on traite les problèmes de transition de phase en introduisant un potentiel thermodynamique, dont chaque minimum est associé à une phase (liquide ou gazeuse, aimantée ou non). On constate alors que le système évolue vers l'état de plus basse énergie. Si l'on prend comme paramètre externe la température, on observe effectivement des valeurs catastrophiques en dessous desquelles le système change de phase : un gaz se liquéfie, une substance ferromagnétique se réaimante spontanément. Dans la figure C, à l'aller comme au retour, le saut aura lieu en p = 0. Le graphique permet de dire que, tant que p est non nul, la règle de Maxwell suffit à déterminer l'état du système. Les phénomènes d'hystérésis liés au retard disparaissent, il n'y a plus effet de mémoire.

Quelle que soit la règle adoptée, si l'on fait varier de façon continue l'excitation p, l'état x du système varie lui aussi de façon continue tant que l'on ne franchit pas une valeur catastrophique (p = ± 8 p = 0). Si l'excitation franchit si peu que ce soit cette valeur, le système change d'état brusquement. La réponse est alors discontinue. Ce saut quantitatif se traduira aux yeux de l'observateur par un changement qualitatif, morphologique, du système. L'analyse précédente reste valable dans le cas général à N variables internes et n paramètres externes.

Les valeurs p1, ..., pn des paramètres externes sont repérés par des points p de l'espace à n dimensions. Pour chacun de ces points, le potentiel F (p1, ..., pn) peut présenter plusieurs minimums locaux en (xi, ..., xN). Chacun d'entre eux représente un équilibre stable. Le système se détermine en fonction de la règle du retard ou de la règle de Maxwell. Mais toutes deux conduisent à la considération de points catastrophiques p, dont le franchissement par les paramètres externes implique un saut des variables internes, et un changement de la morphologie du système. Le lieu de ces points est « l'ensemble des catastrophes », et c'est la géométrie de ce dernier que nous nous proposons d'étudier.

Les ensembles de catastrophes dessinent des surfaces.

Pour faciliter la visualisation de ces « ensembles », nous allons commencer par donner quelques exemples simples, avec trois paramètres, n = 3, seul cas où l'on pourra dessiner la surface décrite par le point représentatif des paramètres.

Les cinq exemples présentés dans l'encadré 2 correspondent à de tels systèmes régis par des potentiels de plus en plus complexes. On leur applique successivement les deux règles. Les trois premières formes obtenues nous sont familières, le pli, la fronce, la queue d'aronde. Les deux autres, les ombilics hyperbolique et elliptique nous sont moins connus, et pourtant un peu d'imagination suffit pour reconnaître un ombilic hyperbolique dans une vague déferlant sur une plage (fig. 3). Dans ce jeu de construction, un système, un potentiel, une surface, pourquoi limiter notre imagination ? On conçoit aisément que l'on pourrait multiplier les exemples à l'infini... Eh bien non ! La beauté de la théorie des catastrophes restreinte réside précisément en ceci que la liste, pour l'essentiel, est close avec ces cinq exemples. On peut imaginer des potentiels plus compliqués ; on peut augmenter le nombre des variables internes. Mais, sauf cas très particuliers, les ensembles de catastrophes que l'on obtiendra seront des combinaisons de nos cinq exemptes. Outre qu'un tel résultat n'est pas intuitif, la difficulté mathématique consiste à lui donner un énoncé précis, puis bien entendu à le démontrer. Il est hors de question de décrire les procédés de démonstration ; tout au plus pouvons-nous indiquer qu'ils reposent sur le théorème des fonctions implicites et le théorème de Sard (fig. 4).

Le résultat fondamental de la théorie des catastrophes peut être énoncé de la façon suivante : pour « presque tous » les systèmes régis par la règle du retard, ou de Maxwell, l'ensemble de catastrophes obtenu en faisant varier simultanément trois paramètres externes est composé uniquement de points plis (simples, doubles ou triples), de points fronce (compliqués éventuellement de points plis), et de queues d'aronde, d'ombilics hyperboliques ou elliptiques (fig. 5). On a un énoncé analogue pour la convention de Maxwell.

L'expression « presque tous » doit être comprise de la façon suivante « si un système ne possède pas la propriété indiqués, une très légère perturbation du potentiel suffit à la rétablir ». Le théorème fondamental, énoncé ici en dimension n = 3, s'étend sans difficulté aux dimensions n = 2 et n = 1. Pour presque tous tes systèmes à deux entrées, l'ensemble de catastrophes, qui est alors une courbe tracée dans le plan (p1, p2), ne comporte que des points plis ou des points fronce. De même, avec des systèmes à une entrée, on obtient en général des points plis uniquement.

Ce théorème s'étend aussi à la dimension 4, à condition de compléter la liste donnée par deux nouveaux éléments, le « papillon » et l' « ombilic parabolique » (encadré 2). Ainsi est close la liste des sept « catastrophes élémentaires », permettant de reconstituer les ensembles de catastrophes les plus généraux en dimension n ¾ 4.

Pour passer à la dimension 5, il faudrait ajouter à la liste une infinité de termes, ce qui lui ôterait du même coup tout intérêt : à quoi servirait un catalogue ayant une infinité de pages ? C'est même le fait le plus étonnant de cette théorie, que cette possibilité de classer les catastrophes quadridimensionnelles en un nombre fini de types. Notons que 4 est aussi la dimension de l'espace temps. On peut se demander si cette coïncidence est fortuite...

Une théorie qui modélise l'action et la réaction d'un système.

La théorie des catastrophes restreinte est avant tout une théorie de l'action ; ce n'est pas le système en soi qui l'intéresse, avec ses multiples variables internes et son potentiel, mais sa réaction à des excitations extérieures définies, décrites au plus par quatre paramètres. Elle n'apporte ni une connaissance du système lui-même, ni une connaissance des stimulus extérieurs, mais une connaissance de la réponse de l'un aux autres. Elle en tire ses limites : la connaissance acquise pour un certain stimulus n'est pas transposable à un autre. Mais elle en tire aussi son universalité : quel que soit le système considéré, pourvu qu'on se borne à quatre paramètres variant simultanément, on peut dire a priori quelles sont les formes dont la composition permettra de reconstituer l'ensemble des catastrophes.

La nature ne s'y conforme pas toujours. Mais, si un système exhibe des formes plus compliquées, c'est que le potentiel a une forme trop particulière pour qu'il n'y ait pas une raison cachée. C'est cette dernière qu'il faut alors rechercher. Il peut s'agir par exemple d'une symétrie à respecter, ou d'un paramètre supplémentaire à incorporer. Même quand la nature se conforme aux prédictions de la théorie, il n'est pas facile de reconnaître dans telle forme innocente une fronce ou un ombilic ; car tes stimulus naturels peuvent être insoupçonnés, les paramètres externes p1, ..., pn aussi cachés que les variables internes aux yeux de l'observateur, qui verra donc le résultat de l'action sans se douter de la logique profonde qui la dirige.

Le moment est venu de donner un exemple. René Thom lui-même en a fourni un certain nombre, sur lesquels nous aurons l'occasion de revenir. La légende veut d'ailleurs qu'il ait découvert la théorie des catastrophes en faisant jouer les reflets du soleil dans une tasse de café : on voit apparaître, dessinés par les caustiques, les cinq catastrophes élémentaires en dimension 3. Mais c'est l'Anglais Christopher Zeeman, autre mathématicien de valeur, qui s'est attaché à dépister systématiquement les exemples naturels de catastrophes, particulièrement de la fronce. Parmi ces exemples, l'un des plus remarquables est celui du muscle cardiaque. Quel plus bel exemple, en effet, de réponses discontinues que ce cœur qui bat dans notre poitrine ? (encadré 3). Pour le physiologiste, le cœur est une pompe qui fait circuler le sang dans deux circuits successifs, irriguant l'un les poumons (petite circulation), l'autre le reste du corps (grande circulation). Quels paramètres de contrôle faut-il dès lors choisir ? Sur quel système agissent-ils ? En l'occurrence, le système est une fibre du myocarde. L'expérience montre qu'une telle fibre a essentiellement deux états (deux puits de potentiel) un état contracté et un état relâché, le passage du premier au second (systole) étant déclenché par un stimulus extérieur, le retour du second au premier (diastole) étant spontané. Le stimulus est fourni périodiquement par un tissu myocardique particulier, le tissu nodal. Mais ce stimulus nerveux n'est pas le seul paramètre dont dépendent les battements cardiaques. La pression intracardiaque joue également un rôle important. Si, par exemple, elle tombe au-dessous d'un certain niveau, ou au contraire dépasse une valeur limite, les contractions n'ont plus lieu. En fonctionnement normal la loi de Starling s'applique. Suivant celle-ci, plus les fibres myocardiques sont étirées en diastole, plus elles se contracteront en systole. Le résultat global sera une augmentation du débit cardiaque, qui pourra passer de 6 litres à 20 litres par minute.

Compte tenu de ces données, la démarche de Zeeman a été la suivante. Voici un système, la fibre myocardique, qui réagit visiblement à deux paramètres externes, le stimulus nerveux et la tension appliquée. Zeeman a donc essayé de le modéliser par une fronce, en adoptant la convention du retard, qui semble la plus naturelle. On est loin de pouvoir expliciter la dynamique interne, c'est-à-dire l'ensemble des équations régissant le phénomène, a fortiori de vérifier qu'elles dérivent d'un potentiel. Disposant de ce modèle, il faut tout d'abord mesurer les paramètres externes : t, la tension appliquée à la fibre, u, le stimulus nerveux. Le choix d'autres paramètres était possible, mais il fallait en faire un. La multitude des variables internes sera résumée en une seule variable significative, notée x, qui peut être par exemple la longueur de la fibre. A chaque couple (t, u) est associée une valeur de x. On obtient ainsi une surface dans l'espace des (t, u, x) dont le contour apparent sur le plan des (t, u) est l'ensemble de catastrophes proprement dit. Une première approximation du fonctionnement in situ consiste à supposer que t est constant et que u est brusquement porté à une valeur u1 puis retombe progressivement à une valeur u0. On a donc pratiqué quatre coupes de la fronce, correspondant à quatre valeurs différentes de t, pour lesquelles on décrit le fonctionnement (figures de l'encadré 3). Le modèle de la fronce permet de rentrer dans des détails beaucoup plus minutieux et de rendre compte avec plus de précision du fonctionnement cardiaque, particulièrement si l'on ne se limite pas au comportement d'une seule fibre.

Toute la complexité bioélectrochimique du phénomène est mise entre parenthèses. C'est là l'apport propre de la théorie des catastrophes, sa force et sa faiblesse. Sa faiblesse, car après tout c'est la réalité qui est ainsi passée sous silence, et le modèle de Zeeman ne nous dit pas pourquoi le cœur bat. Sa force, car même au niveau élémentaire où nous nous sommes placé, qui pourrait nier que ce modèle nous permet de mieux comprendre comment le cœur bat ?

Une première tentative d'utilisation de la théorie des catastrophes permet de mieux comprendre pourquoi le cœur bat

3. Le modèle du cœur

A. L'organe et son fonctionnement

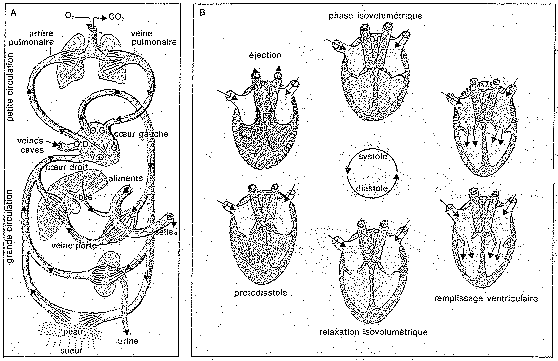
Afin de réaliser le modèle, II faut d'abord définir le système. Celui-ci comprend la grande et la petite circulation (fig. A). La première assure l'approvisionnement en oxygène (O2) et s'effectue sous basse pression. La seconde répartit cet oxygène dans le corps et se fait sous haute pression, de façon à faire remonter le sang aux extrémités, lors de la station verticale. Le cœur lui-même est divisé en deux parties : la droite, qui est le moteur de la petite circulation, et la gauche, qui est le moteur de la grande circulation. Chacune de ces parties présente deux cavités successives, oreillette (O) et ventricule (V), et une paroi musculaire, le myocarde. Son épaisseur est triple au niveau du VG. C'est ce qui créera la différence de pression observée. En effet, ce sont les contractions et les détentes brusques du myocarde qui constituent les battements cardiaques. Du fait des contractions des oreillettes ou des ventricules, le sang est chassé du cœur (fig. 8). Au contraire, il y pénètre lors des détentes. Enfin, un système de valvules convenablement orientées assure le bon fonctionnement de l'ensemble.

B. Le modèle mathématique : la fronce

Le système de référence pour le modèle mathématique sera une fibre musculaire du myocarde. Son excitabilité et sa contractibilité dépendent de deux paramètres. Le premier est de nature électrochimique : il se manifeste par une dépolarisation de la membrane entourant la fibre, et par le transit à travers celle-ci des ions sodium et potassium. Le second est la pression intracardiaque qui crée une tension sur la fibre. Pour traduire ces deux stimulus, nous adopterons les deux paramètres externes suivants u = différence de potentiel à travers la membrane ; t = la tension appliquée. Tous deux agissent sur une variable interne x, ta longueur de la fibre (celle-ci sera toujours repérée en coordonnée verticale).

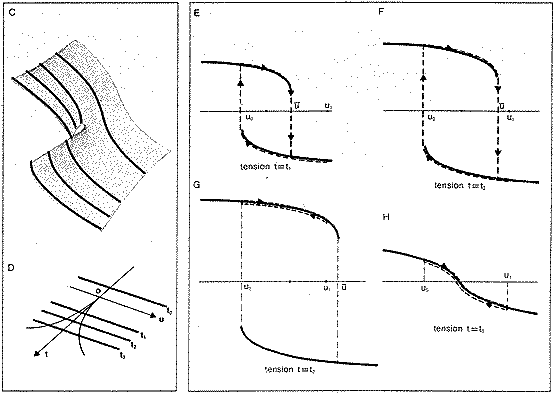
Le modèle alors proposé est celui de la fronce (fig. C). Peut-il décrire le fonctionnement du cœur ? Pour cela observons les quatre sections du modèle par des plans à t = constante (fig. D). On remarque que l'amplitude et l'allure des contractions sont très différentes dans chaque cas (fig. E à H) en dépit du fait que le stimulus nerveux u1-u0 reste inchangé.
Les figures E et F représentent un fonctionnement normal, sous deux tensions t1¾ t2. Le premier cas serait celui d'une fibre auriculaire le second d'une fibre ventriculaire. Le passage de u0 à u1 c'est-à-dire la dépolarisation de la membrane, déclenche la systole. Le retour progressif de u1 à u0 déclenche la diastole. On note l'existence d'un seuil d'excitabilité ù (u barre) de la fibre, en deçà duquel le stimulus est inefficace.
La figure G représente le dysfonctionnement dû à une tension t = t3 trop forte. Le seuil u atteint une valeur telle qu'elle dépasse la valeur maximale u1 du stimulus, rendu de ce fait inopérant. La fibre oscille faiblement autour de sa longueur maximale, mais ne se contracte plus.
La figure H représente le dysfonctionnement dû à une tension t = t0 trop faible. La courbe de réponse s'est tout simplement dépliée, il n'y a plus ni diastole ni systole. Toutes les deux sont remplacées par une contraction rapide et une détente lente, calquées sur les variations du stimulus nerveux, tout à fait inadéquates pour que le cœur joue son rôle de pompe.

Un vieux rêve : recréer l'infinie succession des formes naturelles.

Ne voir dans la théorie des catastrophes qu'une méthode d'analyse des systèmes limiterait beaucoup son impact. L'école britannique développe cet aspect, mais ce n'était pas l'orientation originelle du projet de René Thom. Celle-ci est assez bien indiquée par le titre de son livre, Stabilité structurelle et morphogenèse. La thèse qu'il soutient est que les formes décrites par la théorie des catastrophes, et en particulier les sept catastrophes élémentaires, sont les formes élémentaires dont les combinaisons permettent de recréer l'infinie succession des formes naturelles. Celle-ci n'est pas contingente, ni soumise au hasard, il y a une création des formes, une morphogenèse, dont la logique interne est la théorie mathématique de la stabilité structurelle.

Ce sont les cinq solides réguliers qui ont constitué depuis les Grecs le support géométrique de notre vision de l'univers. Ils sont encore aujourd'hui à la base de notre intuition de l'espace physique : nous ne concevons pas de meilleure manière de l'occuper que par des cubes. De ce point de vue, ce que propose la théorie des catastrophes est un renouvellement, ou tout au moins un enrichissement, de notre bagage intuitif. Dans le monde de Platon comme dans celui de R. Thom, nul n'entre s'il n'est géomètre. Pour Platon, le Démiurge construit le monde en se pliant à la nécessité des cinq solides réguliers. Pour René Thom, la nature parie une langue dont les sept catastrophes élémentaires sont les mots.

La théorie des catastrophes généralisée (titre ajouté par le copiste)

Ce dernier point n'est que partiellement vrai : c'est ici qu'apparaît la théorie des catastrophes généralisée. Celle-ci conserve la première hypothèse de la théorie restreinte (le temps interne s'écoule très rapidement), mais abandonne la seconde (le champ dérive d'un potentiel).

Cela étend considérablement l'éventail de possibilités offertes à l'état interne xl, ..., xN, qui n'est plus contraint de ruisseler le long des pentes du potentiel F et finalement de se retrouver en un minimum local. II peut exister par exemple des orbites périodiques, des oscillations régulières des variables internes qui repassent indéfiniment par les mêmes valeurs. On conçoit que les catastrophes dites métaboliques (fig. 6), obtenues à partir de systèmes dynamiques, soient d'une complexité qui dépasse de beaucoup les catastrophes statiques obtenues comme précédemment à partir de simples potentiels. On n'est d'ailleurs pas actuellement capable de compléter la liste des sept catastrophes élémentaires de manière à bâtir un catalogue de composants auxquels se ramèneraient toutes les catastrophes métaboliques.

Le postulat de base est que la forme sous laquelle tout objet apparaît à un observateur n'est autre que l'ensemble de catastrophes associé à une certaine dynamique (fig. 7). C'est ainsi que la frontière le séparant du milieu extérieur, dans les régions où elle ne présente pas d'accident, sera le plus souvent associée à une catastrophe de type pli. Mais elle peut se creuser d'un sillon, s'exfolier en une cloque, émettre un cil, auquel cas il faudra faire appel à la fronce, à la queue d'aronde, à l'ombilic elliptique. Enfin, bien des situations complexes peuvent être rencontrées, que seule la théorie généralisée peut décrire : catastrophes à bulles, à grumeaux, laminaires, filamenteuses. Elles font partie de notre paysage quotidien, au point que nous n'y prêtons même plus attention : c'est l'écume d'un bock de bière, c'est la condensation en pluie d'un nuage, ce sont les lézardes d'un vieux mur, ce sont les dessins laissés sur le sable par la marée descendante. La théorie de René Thom ne requiert d'ailleurs nullement que ce système dynamique ait une réalité physique. Il le rejette même dans le domaine des idées. C'est ainsi que la forme d'une vague déferlant sur une plage évoque irrésistiblement l'ombilic hyperbolique ; mais personne n'a pu encore donner à cette analogie une quelconque justification hydrodynamique.

L'application quantitative de la théorie des catastrophes aux sciences humaines est un exercice dangereux.

La théorie des catastrophes est-elle une science expérimentale ?

La question de savoir si ta théorie des catastrophes constitue une science expérimentale est d'une grande importance. Une polémique s'est ouverte à ce sujet entre Thom et Zeeman. Pour Zeeman, si la théorie des catastrophes contient une part de vérité, elle doit pouvoir se traduire par des modèles contrôlables expérimentalement. Malheureusement, on constate que si l'accord qualitatif global ne fait pas de doute en général, l'ajustement quantitatif devient de plus en plus mauvais au fur et à mesure que l'on s'éloigne des sciences exactes, au point de devenir franchement aventureux dans le cas des sciences humaines. Un autre reproche que l'on peut faire à Zeeman est de se limiter aux catastrophes élémentaires, comme dans le cas du modèle des mutineries dans les prisons qu'il a proposé avec ses collaborateurs. (3) Ce modèle a d'ailleurs fait récemment l'objet de critiques très sévères. (2)

De son côté, Thom adopte un point de vue opposé à celui de Zeeman. Certes, il considère que les bases mathématiques de la théorie restreinte sont extrêmement solides;- et qu'elle peut fournir de certaines situations physiques, chimiques, voire biologiques, des modèles exacts extrêmement précieux. Mais, selon lui, c'est défigurer la théorie que d'en écarter la notion de catastrophe métabolique qui traduit la dynamique des systèmes, et c'est dénaturer le projet que d'en faire un réservoir d'idées pour expérimentateurs.

La théorie des catastrophes est un regard posé sur le monde. Certes, ce regard ne date pas d'hier, c'est celui même d'Héraclite, pour qui le combat était le père de toutes choses, et qui voyait dans le monde le théâtre sans cesse changeant de l'affrontement des contraires. La théorie des catastrophes exprime cela aujourd'hui en disant que toute forme résulte d'un conflit d'attracteurs. Elle donne des phénomènes non pas une explication, mais une compréhension ; elle permet de se les représenter, mais non pas d'agir sur eux; elle rend à l'homme l'unité et le sens de son savoir, des mathématiques au langage et à la philosophie.

Laissons pour finir la parole à René Thom : « Finalement, le choix des phénomènes considérés comme scientifiquement intéressants est sans doute largement arbitraire. La physique actuelle construit des machines énormes pour mettre en évidence des états dont la durée de vie n'excède pas 10-23 seconde. On n'a sans doute pas tort de vouloir, par l'emploi de tous les moyens techniques disponibles, faire l'inventaire de tous les phénomènes accessibles à l'expérience. On peut néanmoins se poser légitimement une question : quantité de phénomènes familiers (au point qu'ils n'en attirent plus l'attention !) sont cependant de théorie difficile ; par exemple les lézardes d'un vieux mur, la forme d'un nuage, la chute d'une feuille morte, l'écume d'un bock de bière... Qui sait si une réflexion mathématique un peu plus poussée sur ce genre de petits phénomènes ne se révélerait pas, finalement, plus profitable à la science ? »

Références:
(1) Science, 196, 287, 1977.
(2) Sussman, Zahler, « Catastrophe theory as applied to the social and biological sciences », Synthèse, preprint fév. 1977
(3) Hall, Harrison, Marriage, Schapland, Zeeman, « A model for prison disturbancies », Journal of Math. and star. Psychology (1976).

Pour en savoir plus
  • C. Zeeman, « Differential equations for the heartbeat and nerve impulse », publié dans Dynamical systems, Peixoto (ed.), Academic Press, 1973, p, 683-741. Un article à la portée du non-initié, mais limité à la théorie restreinte.
  • On growth and form, d'Arcy Thomson, ouvrage consacré à la richesse des formes naturelles et à leurs transformations réciproques, éd. abrégée, Cambridge University Press, Oxford, 1961.
  • Le point de vue des adversaires : Sussmann et Zahler ont publié dans Synthèse une violente attaque de la théorie, plus particulièrement dirigée contre Zeeman. (2)
  • Sur les positions épistémologiques de René Thom, voir Stabilité structurelle et morphogénèse, Benjamin, 1972 ; et « La science malgré tout », Encyclopaedia universalis, vol. 17.
  • Un exposé plus technique de la théorie des catastrophes : Sussman, « Catastrophe theory », Synthèse, 31, n° 2. 229, 1975.
·