|
retour Une théorie des modèles de René Thom, page complémentaire sur les modèles catastrophiques, page d'accueil du site |
||||
|
1 |
1 Sources œuvres complètes de René Thom, CD Rom IEHS Encyclopedia Universalis un colloque de l'ENS: Journée Trois corps, classique-quantique, discret-continu, organisé par : Giuseppe Longo (CNRS) et Thierry Paul (ENS) et notamment la table ronde des 28 et 29 septembre 2004 accessibles sur internet (http://www.diffusion.ens.fr/index.php ?res=cycles&idcycle=109). Lors de la première table ronde, avec Jean Petitot (qui rappelle l'apport de Thom), Yves-Marie Visetti (très accessible; il fait une remarque sur la TC qui mérite d'être écoutée), Thierry Paul, Carles Simo, Dominique Delande, Annick Lesne et Jean-Michel Salanskis (si sa première présentation des différentes conceptions du continu n'est pas facile à suivre, sa remarque à 1:37:01 (fichier .mov de 1,8 Mo à télécharger) me semble très claire même s'il la qualifie de journalistique et facile: "ce qui fonctionne comme language commun c'est le continu de Cantor-Dedekin", c'est-à-dire celui de la majorité des mathématiciens; cependant "il y a un autre moyen de communication c'est Aristote"...). |
|||
|
1. Le continu s'oppose au discret plutôt qu'au discontinu |
||||
|
Définition
habituelle du
continu: Ainsi, et même si ce n'est que d'une façon secondaire, cette définition reste une étape importante pour les élèves : la continuité s'oppose à la discontinuité. La continuité s'exprime pour l'élève comme une propriété graphique de la fonction qui est représentée par une ligne continue (par opposition à une ligne discontinue). Mais cette représentation est en fait une bonne image du l'opposition continu / discret. |
|
Une application continue en un point prend des valeurs qui ne contrastent pas avec celles qu'elle prend au voisinage de ce point - à l'inverse, une application discontinue présente des valeurs qui peuvent être très différentes en un point et en un de ses voisinages. En classe de terminale S on approche les notions de continuité en un point [f est continue en un point a de R de son ensemble de définition lorsque la limite de f en a existe et vaut f(a)] et continuité sur un intervalle [f est continue sur un intervalle I inclus dans son domaine de définition lorsqu'elle est continue en tout point a de R appartenant à I]. On admet ensuite sans le démontrer que les fonctions polynômes, rationnelles, trigonométriques, logarithmes, exponentielles, racine carrée, valeur absolue ainsi que les fonctions obtenues par opérations algébriques sur ces fonctions ... sont TOUTES CONTINUES sur tout intervalle contenu dans leur ensemble de définition. |
|
Mais, d'une façon plus générale et donc topologiquement, le continu s'oppose au discret. Par exemple l'ensemble des nombres réels R est continu (représentons-le par une ligne continue _______________ ) alors que Z, ensemble des entiers relatifs est discontinu ou discret (et peut être représenté par une ligne discontinue .......................... de points); R est un espace dit connexe et Z est dit discret; la richesse du problème posé par ces différences fait l'objet d'un questionnement toujours actuel. |
| |
|
René Thom, peut être qualifié de "penseur du continu" (voir une interview de Petitot dans La Recherche: http://www.larecherche.fr/ special/web/web360.html); il utilise, en plus des concepts mathématiques familiers aux topologues, la distinction qu'Aristote fait entre Genre et espèce (voir par exemple les parties de 1 à 4 dans Réflexions sur le continu de Hansjakob Seiler, 1992, in Colloque sur le continu linguistique, Caen, 22-24 juin 1992, 1992f7.pdf - dont voici quelques éléments du résumé). Le continu est ontologiquement antérieur au discret. En effet, il est très facile pour un continu d'admettre des accidents discrets (exemple : une ligne brisée), alors qu'un objet discret ne peut admettre un accident continu sans être lui-même continu. Objection des continus à singularités denses (en mathématique : la droite réelle). Du continu pur, on ne peut rien dire (c'est la forme la plus pauvre d'existence). Seuls les accidents discrets portés par le continu peuvent motiver un discours. . . L'accident discret minimal : le point sur la droite. La distinction d'Aristote entre point « virtuel » (en puissance) et point réel (en acte). Le point réel sépare l'axe en deux demi-axes. L'acte sépare. C'est la séparation dichotomique qui permet de passer de un à deux. Cette scission possède un modèle algébrique issu d'une dynamique continue, c'est la singularité « fourche » définie par l'équation v = 0 dans le modèle fronce de la Théorie des catastrophes, d'équation V = x4/4 + ux2/2 + vx. La singularité fourche 1, d'équation x3 + ux + v = 0, est à l'origine du symbolisme de la flèche, symbole d'irréversibilité. En effet il est plus facile d'aller de 2 en 1 par un chemin continu que de 1 en 2 : à la fourche, il faut faire un choix (en principe arbitraire) : et c'est difficile, dans un univers où Dieu ne joue pas aux dés. . . La notion aristotélicienne de genre (Grec Genos): on désigne ainsi un ensemble de concepts qui sont sémantiquement fortement apparentés. Sous la forme la plus pure, comme dans le genre des adjectifs de couleur, on peut par expérience mentale transformer continûment un attribut a en un autre attribut b du même genre. Mais il y a des genres (comme les relations de parentés), où cette continuité n'existe pas ; elle est remplacée par une dynamique canonique (discrète) entre les concepts. Pour Aristote le genre est « comme une matière », c'est un continu qui se sépare « canoniquement » en morceaux, chacun des morceaux est une espèce (eidos) ; cette scission de la matière du genre est réalisée par une coupure, la différence spécifique. Seules les catégories sont individuellement séparées, elles constituent une «matière discrète ». Dans une optique évolutionniste, on peut considérer que la décomposition d'un genre en espèces a une origine préverbale dans la correspondance Stimulus ---> Réponse chez l'animal. Les stimuli sont des objets continus alors que les grandes stratégies de réponse forment un ensemble discret fini (par exemple : Attaque - Fuite, Indifférence). Un stimulus est « prégnant » s'il suscite une réponse (attractive ou répulsive) immédiate. |
||
|
2. Réintroduire du continu en SVT |
||||
|
La compréhension des mécanismes biologiques fait appel habituellement à des modèles discontinus au sens de discrets. Mais des modèles comme ceux proposés par Thom permettent de réintroduire le continu en SVT, ce qui me semble un projet réalisable. |
|
Je m'explique : une raison simple pour laquelle la biologie a un besoin absolu de continu est la présence du temps. Le temps du vivant est un continu (voir page sur le temps du programme de terminale S). La nécessité d'introduire le temps apparaît de façon particulièrement claire aux les élèves de 1èreS habitués à tracer le temps en abscisse de tant de courbes en classe de physique. Interrogé sur la présence du temps comme paramètre dans les modèles thomiens, je leur avais répondu à ce moment là que le temps est sous-entendu mais qu'il n'est que rarement exprimé sous forme de paramètre individualisé (voir cours de 1èreS, nouveau modèle de glycémie). Je complète maintenant cette réponse en affirmant que le temps est bien une trace de ce continu sous-jacent à tout modèle biologique. Il peut être discrétisé pour une expérience par un mécanisme dit "générateur de temps" (sous-entendu "générateur de temps discret" : le chronomètre). En effet le mouvement de balancier ou la pulsation périodique du mécanisme d'horlogerie sépare (la séparation est un acte en philosophie aristotélicienne sur le continu du temps qui est puissance - voir note sur ces notions dans la page sur les 4 causes d'Aristote) des durées par des discontinuités (les bords de chaque période si l'on représente géométriquement le temps par une droite segmentée en périodes). Ce que l'on fait ici pour le temps avec un mécanisme analogique d'horlogerie peut être fait de la même manière pour le vivant par un mécanisme fonctionnel où les formes qui se séparent du fond continu sont les saillances au sens de Thom (pour une approche de ce vocabulaire voir la page sur les 4 causes d'Aristote). Les fonctions du vivant, immergées dans un continu (le continu du temps) ne peuvent être qu'un continu. Ceci à pour conséquence que toute fonction vivante présentant le temps en paramètre (caché ou explicite) doit être continue. |
||
|
|
|
En SVT on fait habituellement appel de façon implicite au discontinu lorsque l'on explicite des propriétés du vivant à l'aide de molécules qui produisent des effets sous le contrôle d'autres molécules, à moins que l'on ne considère chaque molécule qu'en tant qu'élément d'un système mécanique (mais la mécanique au niveau moléculaire n'est pas aussi facilement explicitée qu'au niveau macroscopique: parler de masse, de gravité et de point d'application d'une force est assez délicat au niveau d'une seule molécule... intuitivement on opère une réduction mentale d'échelle mais quelle signification a-t-elle ?). Les molécules sont un ensemble discret. On a beau en imaginer une infinité le problème n'en est pas moins posé et l'infinité (aux bornes) ne génère pas la continuité (l'infinité des molécules est une notion particulièrement fausse en biologie car les molécules cytoplasmiques sont au contraire en quantité bien déterminée, tout à fait dénombrables et localisables: voir page sur la cellule). Un modèle de régulation physiologique qui fait intervenir de très nombreuses molécules, des gènes, et tout autre système matériel que l'on voudra, est ainsi présenté la plupart du temps comme un système discontinu, ce qui est impropre. |
||
| |
|
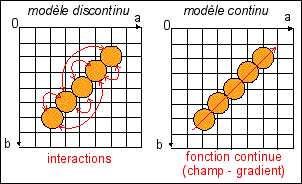
Une illustration d'une interprétation des relations entre des unités (des cellules, des molécules, des individus... en orange), situés dans un plan (a,b) expérimental de contrôle (a et b sont des paramètres mesurables; les unités sont repérées par leurs coordonnées dans le plan de contrôle), par un modèle discontinu de réseau d'interactions (flèches rouges) versus un modèle continu d'une fonction sous-jacente relié par exemple à un champ de vecteurs déterminant un gradient orienté dans le sens de la flèche. |
|
|
| |
|
|
||
| |
|
Dans
un
modèle
discontinu
chaque
unité
présente
des
caractéristiques
qui
résultent
de sa position
dans le
plan (a,b) ;
la forme
globale
résulte
de la
composition de
toutes les
morphologies
individuelles. |
|
Dans
un
modèle
continu
l'étude
géométrique
de la
morphologie
permet d'en
déterminer
les
propriétés
universelles.
La forme
étant
considérée
comme une
donnée
on en explore
les
propriétés
grâce
à des
outils
mathématiques.
On
considère
donc le
gradient comme
une
donnée
sous-jacente
au
système
(une
dynamique
sous-jacente)
et on cherche
à
mathématiser
(localiser) la
fonction
vitale qui lui
a donné
naissance. La
forme est "ce
qui se
sépare
du fond
continu"; les
bords
de la forme
sont stables
(ce sont les
points de
catastrophe
dans la
théorie
des
modèles
de René
Thom). |
| |
|
Cela fait de nombreuses années que les physiciens ont accepté de composer avec ces deux aspects : le discret c'est l'aspect particulaire et le continu c'est l'aspect ondulatoire. La notion de champ permet de modéliser un changement à distance et immatériel que l'on considère comme un transport d'énergie (c'est par exemple le cas des ondes gravitationnelles, support de l'énergie de gravitation, que l'on peut aussi modéliser par une particule: le graviton; même si l'un ou l'autre des deux aspects est souvent beaucoup plus commode et clair). En mathématiques le champ désigne l'ensemble des valeurs prises par une variable. En physique le champ désigne l'ensemble des valeurs d'une grandeur physique en tout point de son espace de d'observation (un espace comprenant souvent le temps comme dimension). La notion de champ en physique a permis de masquer le côté magique d'une action quasi-instantanée à distance en parlant de modification de l'espace-temps pour qualifier les relations entre deux points ou portions de l'espace appartenant au même champ. Il me paraît urgent de faire de même en biologie en proposant des champs morphogénétiques ou des champs fonctionnels, modèles de la propagation des fonctions locales nutritives, relationnelles et reproductives (que Thom a essayé de nommer chréodes à la suite de Waddington, mais le mot n'a pas eu de succès...; en fait le mot chréode (chreod) désignait le support biologique d'un champ morphogénétique, une « route obligatoire » du développement, voir CDRom des œuvres complètes: 1991i.pdf et 1993f7.pdf). Et comme on s'intéresse davantage aux variations des fonctions vitales qu'à leur valeur en un point de l'espace métabolique, Thom utilise principalement le concept de gradient qui est mathématique avant d'être utilisé par les physiciens. Le gradient est un vecteur ayant pour composantes les dérivées partielles d'une fonction, correspondant à sa variation. Pour la fonction de nutrition, le gradient nutritionnel en chaque point de l'espace du métabolisme permet de se faire une idée du champ nutritif d'une organisme. Le concept d'onde en physique est élargi à la biologie par Thom en de nombreuses occasions. Que ce soient les ondes de choc pour désigner des conflits d'attracteurs ou des ondes nutritives ou reproductives qui désignent les changements d'un tissu placé dans un champ morphogénétique. Une formulation mathématique de la notion de front d'onde, applicable à une onde fonctionnelle biologique, est proposée dans 1973f8.pdf (Sur la propagation des fronts d'onde et l'optique géomètrique, 1973). Des exemples pour comprendre la différence entre un modèle continu (le pendule, le culbuto, un oscillateur harmonique ou un modèle moléculaire flip-flop...) et un modèle discontinu (n'importe quel modèle cybernétique ou informatique, la réponse immunitaire à médiation cellulaire telle qu'elle est habituellement présentée, la régulation de la glycémie... id.); il est évident que les modèles biologiques de régulation peuvent aussi être présentés sous une forme continue avec un autre modèle. |
||
|
3. Approche expérimentale et analogique : une pédagogie |
||||
|
EN TRAVAUX août-septembre 2005 Les
paragraphes
qui suivent
ont pour but
d'une part de
préciser
un vocabulaire
inhabituel aux
enseignants de
SVT , et
d'autre part
de mettre
l'accent sur
la
nécessité
de la
formation
mathématique
pour quiconque
souhaite
comprendre des
résultats
expérimentaux. |
|
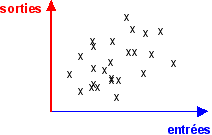
3.1 - Tracer la caractéristique d'un système dynamique c'est faire l'hypothèse d'une fonction continue sous-jacente En reprenant le graphisme utilisé dans la page sur les modèles. Si l'on représente (graphe ci-dessous ) les sorties en fonction des entrées pour un système vivant chaque point définit un état du système (dans l'espace Rn x Rr). |
||
|
|
|
|||
|
Dans une approche discontinue le nuage de points obtenu est interprété statistiquement (voir note) alors que dans une approche continue, les points sont représentatifs d'une application de Rr vers Rn qui est une fonction (CONTINUE) si à une entrée (p1) on ne fait correspondre qu'un nombre fini de sorties (x). La fonction est représentée par un graphe que l'on peut appeler la caractéristique du système (que l'on pourrait définir comme un tracé de la dynamique). Pour un thermodynamicien les x, y... (sorties) sont les solutions du système (sous entendu des équations décrivant le système) dont les p1, p2... (entrées) sont les paramètres. Mais je prendrai surtout des exemples mécaniques qui me sont plus familiers que ceux issus de la thermodynamique. |
||||
|
quelques caractéristiques de systèmes avec une seule variable de contrôle : p |
||||
|
1
|
|
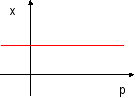
un système stationnaire p peut prendre des valeurs quelconques mais x est figé. Ce système est plus que stable, il est amorphe au sens où sa forme (variable x) est dépourvue de dynamique, même si on peut considérer un paramètre de contrôle... inopérant sur la morphologie. |
||
|
|
||||
|
2
|
|
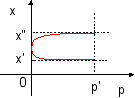
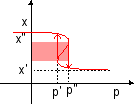
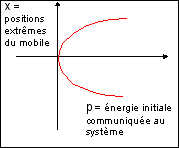
un système à deux positions stables et une bifurcation Le
système
n'est
défini
que pour des
valeurs de p
inférieures
à p'.
La morphologie
(x)
présente
deux
états
stables
habituels (x'
et x") et une
série
d'états
intermédiaires
rarement
atteints
(instables).
En O, point
de bifurcation,
le
système
est instable
et doit
bifurquer vers
l'un où
l'autre des
états
stables. |
Ce
système
correspond
à la
catastrophe pli
de René
Thom. |
|
 Le centre de gravité peut être déplacé grâce à la masse mobile noire fixée sur la bande supérieure. L'état médian (p=0) est très instable (en fait non réalisé dans une machine idéale). Les deux positions extrêmes (pour p=p') et les positions intermédiaires sont stables. |
||||
|
|
||||
|
3
|
|
un système périodique La
caractéristique
est un cycle. |
||
|
|
||||
|
4
|
|
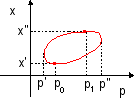
un système en cycle d'hystérésis Ce
système
est
défini
pour toute
valeur de p et
pourtant x ne
peut prendre
que des
valeurs
comprises
entre x' et x"
et plus
particulièrement,
le
système
n'est stable
que pour
lorsqu'il
prend les deux
valeurs x' et
x"; toute
valeur de p
fait
évoluer
rapidement le
système
soit voir x',
soit vers x";
ce qui en fait
un
modèle
de
système
stable
et résistant
à de
petites
perturbations
de p. |
|
Ce système, avec deux paramètres de contrôle (et donc un amortissement de la zone de variation rapide de x), correspond à la catastrophe fronce de René Thom. Une analogie mécanique a été proposée par Zeeman (disque en rotation avec deux élastiques maintenant tour à tour et conjointement une position extrême). Un modèle sous forme d'applet est présenté sur le site de Lucien Dujardin (http://perso.wanadoo.fr/ l.d.v.dujardin/ct/fr _cusp.html). Un modèle avec un seul paramètre de contrôle pourrait être le même montage avec les points de fixation des élastiques (A et C) fixes: seul B peut tourner avec le disque. |
|
Remarque: |
||||
|
L'hystérésis, est définie étymologiquement comme un décalage dans l'évolution d'un phénomène physique par rapport à sa cause (un retard). |
|
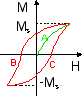
En physique le cycle d'hystérésis est défini pour une substance ferromagnétique qui n'a jamais été aimantée. Si l'on trace son aimantation (M) en fonction de l'intensité du champ magnétique imposé (H), on observe d'abord une aimantation progressive (courbe A) jusqu'à une valeur limite dite aimantation à saturation (Ms). Lorsqu'on fait décroître ensuite le champ jusqu'à une valeur négative très élevée, l'aimantation NE REVIENT PAS À UNE VALEUR NULLE (en décrivant la courbe A en sens inverse) mais décrit la courbe B (c'est cette non réversibilité qui justifie le terme d'hystérésis puisque l'aimantation est "en retard" par rapport à la diminution du champ magnétique). Si l'on applique un champ de sens opposé de plus en plus intense la diminution de l'aimantation se poursuit le long de B jusqu'à la valeur limite (-Ms). Puis, en faisant croître à nouveau le champ, elle décrit la courbe C, symétrique de B par rapport à l'origine 0. Les valeurs de l'aimantation rémanente (qui reste une fois le champ appliqué revenu à la valeur 0) dépendent du chemin suivi: positive si le champ décroît depuis une valeur positive élevée, et négative si le champ croît depuis une valeur fortement négative; ce SYSTÈME A DONC UNE MÉMOIRE du dernier champ élevé appliqué, ce qui peut être ramené à ce que l'on appelle la "sensibilité aux conditions initiales"). |
||
|
|
||||
|
Cas particulier de caractéristique, la cinétique est la représentation d'un paramètre observable (sortie, x) en fonction du temps (entrée, t): x=f(t). Comme on a seulement deux paramètres, les éléments du système sont placés dans un plan (t,x). Pour représenter un mouvement en SVT, comme il est fréquent de le faire en physique, on ne se place plus seulement dans le plan des positions (x=f(t)) (qui permet d'embrasser la cinétique d'un seul coup d'œil) mais dans l'espace des phases où l'on ajoute le paramètre vitesse (v=dx/dt). La dynamique est alors représentée par une trajectoire dans l'espace (x(t),v). |
||||
|
3.2 - De l'intérêt de l'espace des phases où les dynamiques sont représentées par des trajectoires (ou orbites) |
||||
|
Remarques: |
|
L'espace
des phases
est
défini
théoriquement
comme un
espace
abstrait qui
permet de
définir
complètement
l'état
d'un
système
à
partir de la
connaissance
des
coordonnées
de ce
système
dans cet
espace
(article
"turbulence"
EU). |
|
Un attracteur est défini comme une zone de l'espace des phases où le système se trouve après un temps infini: c'est un état asymptotique pour la fonction associée à la dynamique du système. Pour un système donné il peut exister plusieurs attracteurs, dépendant de la zone de l'espace des phases à laquelle appartient la condition initiale. On appelle bassin d'attraction d'un attracteur l'ensemble des conditions initiales (portion de l'espace des phases) qui y conduisent. Une bifurcation du système correspond au passage d'un bassin d'attraction à un autre, et donc d'un attracteur à un autre.
Pour une étude mathématique complète voir l'exemple du pendule simple qui est traité intégralement dans l'Encyclopedia Universalis au chapitre Systèmes dynamiques différentiables (1. Le pendule sans frottement, un système hamiltonien). Le niveau est celui d'un élève d'une classe préparatoire scientifique. Pour une étude préliminaire plus ludique je vais abondamment utiliser ci-après les pages de Lucien Dujardin (avec son accord). Un exemple d'utilisation d'espace des phases en SVT est notamment le travail de Madame Dambricourt-Malassé sur la dynamique crânio-faciale humaine appliquée aux crânes fossiles de la lignée humaine (voir un essai de présentation dans l'ancienne page sur les modèles, mais les modèles mathématiques sont dans des publications spécialisées auxquelles je n'ai pas eu accès, voir bibliographie). |
|
*
Une
dynamique,
c'est un
mouvement. En mathématiques une fonction linéaire est une fonction dont la représentation graphique est une droite. En dynamique les systèmes linéaires sont des systèmes obéissant à des équations aux dérivées partielles linéaires c'est-à-dire qui sont de la forme dxi/dt=∑(j=1,n) ai,j(t) xj + bi(t) (formant un système différentiel linéaire). En utilisant une notation matricielle on peut écrire dx/dt=A(t).x + b(t), avec la matrice A(t)=(aij(t)) et les deux vecteurs x = (x1,...,xj,..., xn) et b(t)= (b1,...,bj,..., bn). On retrouve en effet l'équation d'une droite dans l'espace (x1,...,xj,..., xn, dx1/dt, ...,dxi/dt,...,dxn/dt) qui est l'espace des phases. Par extension on parle d'équations différentielles linéaires du second ordre pour des équations de la forme d2x/dt2 + a(t) dx/dt + b(t) x + c(t) = 0. Une fonction non linéaire a une représentation graphique qui est pas une droite. La dynamique d'un système non linéaire obéit à une équation différentielle de la forme dx/dt = f(x, t); où x est un vecteur de Rn, f est une fonction (non linéaire) continue à valeur dans Rn et t une variable réelle |
|
|||
| |
|
a
-
L'oscillateur
linéaire
non amorti, |
||
| |
|
Ce premier
cas le plus
simple va nous
permettre de
définir
les outils
mathématiques. |
|
Dans le plan des oscillations la trajectoire est une droite. L'espace des phases est alors un plan (produit d'une droite par une droite) (alors que c'est la surface d'un cylindre (de dimension 2 comme le plan) dans le cas du pendule, produit d'un cercle (de dimension 1) par une droite). |
|
L'applet de Lucien Dujardin (http://perso.wanadoo.fr/ l.d.v.dujardin/regul/ osc_lin.html) est exploitée de façon pédagogique par l'auteur. Je la reprends ici. |
|
Le point G représente une masse oscillante (par exemple attachée à deux ressorts et coulissant le long d'un axe horizontal), idéalement sans frottement. |
||
|
|
|
|
Déplacez le point G avec le bouton de la souris enfoncé pour initier le mouvement; observer ensuite les oscillations en relâchant le bouton. (le vecteur vitesse est dessiné en bleu) |
|
|
|
La trajectoire du mobile (G) est un segment de droite dans le plan des oscillations. x est défini par la position du mobile par rapport à la position de repos (0). x0 définit à l'instant t0 la position initiale (et donc l'énergie communiquée au mobile). |
|
Dans le plan des oscillations la trace est peu commode car la même position est occupée à des instants différents. On cherche donc à utiliser un espace paramètré par le temps. On peut utiliser ce que l'on peut appeler le plan des positions (t,x). 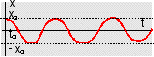 La trajectoire du mobile (G) est une sinusoïde dans le plan des positions (t,x). Cette représentation met en valeur le caractère périodique du mouvement. |
|
|
|
|
|||
|
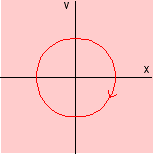
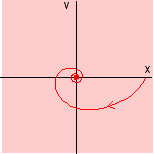
Dans le plan des phases (x,v) la trajectoire devient un cercle. C'est la courbe intégrale ou l'orbite du mouvement (c'est une courbe géométrique orientée). L'ensemble des orbites (ou courbes intégrales) dans l'espace des phases est appelé portait de phase. Une propriété essentielle des orbites est de ne pouvoir s'intersecter. Nous ne représenterons qu'une seule orbite possible. Pour voir sa trace utilisez dans le cadre ci-dessous la même applet de L. Dujardin (étendue). |
|
|
|
une trajectoire possible moyenne a été représentée
la dynamique périodique est stable et présente la forme d'un cycle (attracteur cyclique) |
|
|
Si l'on représente géométriquement l'ensemble des trajectoires possibles on a la forme suivante: 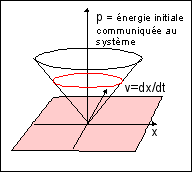 L'énergie initiale (p) communiquée au mobile (G) est conservée (système conservatif) puisque les frottements sont considérés comme nuls. |
|
La caractéristique d'un tel système (voir ci-dessus) est la représentation de la morphologie (x, amplitude des oscillations) ou (x, position extrême du mobile) en fonction d'un paramètre de contrôle (p), ici l'énergie communiquée au mobile (proportionnelle à x0). C'est donc une figure voisine de la précédente mais dans un plan et avec l'axe des p horizontal. La morphologie est stable, pour un niveau d'énergie donnée. Cette morphologie est qualifiée de pli. 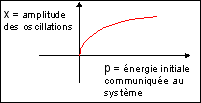
|
|
|
Remarque1
: Remarque 2: ce système est non dissipatif car, idéalement, il ne perd aucune énergie ni sous forme de chaleur ni sous forme de frottement. Un système non dissipatif peut soit diverger dans l'espace des phases soit présenter une dynamique stable (ici une dynamique périodique avec un attracteur de type cycle), soit enfin avoir un comportement chaotique. On va maintenant s'intéresser à une système dissipatif. |
|
Les équations du mouvement sont accessibles à un élève de terminale S (et même de première S). Pour une approche ludique vous pouvez aussi utiliser l'applet "Oscillateur harmonique" de l'Encyclopedia Universalis (version 10) qui montre la similitude du mouvement circulaire uniforme d'un point et de l'oscillation harmonique d'une masse accrochée à un ressort.
Lucien Dujardin présente (http://perso.wanadoo.fr/ l.d.v.dujardin/ regul/ VdP_index1.html) un modèle analogique électrique d'un système oscillant dans l'espace (q,i), q étant la charge électrique d'un condensateur (C) et i le courant passant dans le montage (le circuit comporte une self (L) et un condensateur). Vous pouvez aussi vous référer à l'article "oscillateurs" de l'Encyclopedia Universalis. L'oscillateur harmonique simple obéit à l'équation différentielle q"+q/(L.C) = 0. On a donc encore une fois la même équation différentielle. avec cette fois w = 1/(L.C). |
||
|
|
L'intérêt
de
géométriser
le mouvement
et d'utiliser
l'espace des
phases et donc
que l'on peut
s'affranchir
de la nature
du
système.
Les
caractéristiques
géométriques
de la
dynamique
s'appliquent
aussi bien
à un
système
mécanique
qu'à un
système
électrique.
Il n'y a qu'un
pas à
franchir pour
affirmer que
l'on
peut aussi
l'appliquer
à un
système
biologique.
Il a plusieurs
systèmes
biologiques
qui me
paraissent
présenter
des mouvements
oscillants non
amortis (ne
serait-ce que
la contraction
d'une fibre
cardiaque,
mais je pense
aussi à
des structures
moléculaires
membranaires
oscillantes
imaginées
par les
biochimistes...)
mais on a pris
l'habitude de
considérer
que comme tout
système
mécanique
connu les
frottements ne
sont pas
négligeables
et qu'il y a
donc
obligatoirement
un
mécanisme
d'apport
d'énergie
pour
entretenir le
mouvement.
Cette vision
est
peut-être
en train de
changer car on
observe
maintenant des
systèmes
qui semblent
avoir un
frottement nul
(c'est la
suprafriction
ou frottement
inférieur
à la
limite
mesurable; voir
Vers le
frottement
zéro,
Jean-Michel
Martin, Pour
la Science,
334,
août
2005, pp62-67).
Dois-je
spécifier
que la
physique de la
friction entre
systèmes
moléculaires
intracytoplasmiques
ou
membranaires
est encore
inaccessible ?
Rien
n'interdit de
poser,
macroscopiquement
l'hypothèse
du frottement
zéro
dans certains
systèmes
biologiques.
Bien
évidemment,
considérer
la fibre
cardiaque
comme un
oscillateur
non amorti
n'apporte pas
grand-chose de
premier abord
(nous allons y
revenir) mais
c'est la
démarche
qu'il faut
retenir:
comprendre
c'est
mathématiser
le
comportement
et expliciter
analogiquement
(ici
mécaniquement)
un
phénomène. |
|||
|
|
EN
COURS On a pris l'habitude de rapporter l'état physiologique de la fibre à la mesure de la différence de potentiel entre l'intérieur de la fibre (microélectrode intracytoplasmique) et le milieu extérieur. Typiquement la fibre oscille entre deux états : repos et excité. Les deux états ne sont pas du tout de même durée. La contraction musculaire peut être modélisée par un cycle catastrophique que nous aurons l'occasion de revoir (voir par exemple l'article d'Ivar Ekeland en attendant). Mais on peut utiliser d'autres variables pour ne considérer que la périodicité du système qui doit obéir à l'équation différentielle x"+wx=0. |
|||
| |
|
b - L'oscillateur linéaire amorti, un système dynamique stable qui tend vers un état stationnaire |
||
|
L'intérêt du système oscillant amorti est que c'est un système dynamique stable tendant vers un état stationnaire au sens où il tend naturellement à revenir à sa position de repos après une perturbation. Ce qui est très important pour tous les phénomènes de régulation. J'utilise à nouveau ici le travail de Monsieur Dujardin. |
|
Le point G représente une masse oscillante à oscillations amorties, par exemple avec frottement. |
||
|
|
|
|
Déplacez le point G avec le bouton de la souris enfoncé pour initier le mouvement; observer ensuite les oscillations en relâchant le bouton. (le vecteur vitesse est dessiné en bleu) |
|
|
|
La trajectoire du mobile (G) est encore un segment de droite dans le plan des oscillations. e désigne la diminution de l'amplitude du mouvement liée à l'amortissement. |
|
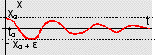 La trajectoire du mobile (G) est une sinusoïde amortie dans le plan des positions (t,x). |
|
|
Remarque: |
|
|
|
une trajectoire possible a été représentée
|
|
|
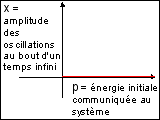
La caractéristique d'un tel système (voir ci-dessus) est la représentation de la morphologie en fonction d'un paramètre de contrôle, ici l'énergie communiquée au mobile (proportionnelle à x0). La morphologie, amplitude des oscillations au bout d'un temps "infini", est toujours identique, c'est le point stationnaire. La caractéristique est ici une droite de pente nulle. En fait, le paramètre de contrôle est inopérant. |
|
 |
|
|
|
|
c . un système dynamique expérimental linéaire à caractéristique modulable On peut construire un système dynamique expérimental qui conjugue les propriétés des deux systèmes précédents à l'aide d'un paramètre supplémentaire opératoire. Pour reprendre l'exemple du pendule, on peut considérer un pendule amorti (avec frottement) mais aussi accéléré (par exemple pour lequel on puisse communiquer une impulsion modulable à chaque passage en un point fixe... comme le coup d'archet sur la corde vibrante). On peut donc maintenir à volonté soit des oscillations amorties (système dissipatif), soit accélérées (système conservatif ou entretenu; à la limite on peut compenser exactement les frottements). Les équations sont complexes et les mathématiques déjà ardues dans le cas général. (voir EU, Systèmes dynamiques différentiables, 3 - bifurcations de cycles-limites et auto-oscillations) |
||
|
|
Le système obéit à l'équation différentielle: q"+ q'. (r-R0)/L + q/L.C = 0. L'applet trace directement l'orbite en pointillés dans l'espace des phases (q,q'), soit (q,i) puisque i = q' = dq/dt. Dans la partie supérieure (rectangle gris) on peut suivre les oscillations de la valeur de q (matérialisée par le point G) en fonction du temps |
|||
|
Un
exemple
d'applet avec
commande
externe |
|
L'oscillateur électronique représenté permet, en faisant varier la résistance (R0) du système, d'obtenir des orbites :
ou divergentes (R0> r = 5); un excès d'énergie est fourni au système (pas d'attracteur mais au contraire un point fixe qui joue le rôle de répulseur). + |
||
|
|
||||
|
|
|
|||
|
La
caractéristique
du
système
ne peut
être
tracée
que dans un
espace
à 3
dimensions... |
||||
|
|
|
d - un système dynamique non linéaire avec cycle limite à la suite d'une bifurcation de Hopf |
||
|
|
Le système précédent n'est pas vraiment utilisable comme modèle dynamique du vivant. Un système divergent n'est pas très conseillé pour un être vivant. Tout comme un système qui présente un attracteur ponctuel, du moins dans les cas les plus courants (il faut une stabilité mais pas un état stationnaire). Pour éviter que le système ne puisse diverger, un des moyens les plus employés en dynamique est l'introduction d'un terme en (x2-1) à la place de (r-R0), ce qui rend l'équation différentielle du système non linéaire. Comme il faut de plus que la perturbation soit faible pour ne pas amortir le système il faut ajouter un petit facteur (µ) au terme en (x2-1). La plus étudiée des équations différentielle de ce type est l'équation de Van der Pol (1920) : où µ est un (petit) paramètre. |
|
Dès
les
années
1880, Henri
Poincaré
avait
montré
que toute
courbe
intégrale
du champ
défini
par
équation
différentielle
d'ordre 1 sur
la
sphère
soit aboutit
à un
point critique
(nœud,
selle, etc.),
soit devient
asymptotique
à une
courbe
fermée
tangente au
champ, qu'on
appelle cycle
limite. Si l'on reprend l'exemple précédent dans le domaine électrique comme l'a fait Lucien Dujardin on obtient ce que l'on appelle le circuit de Van der Pol (couplage inductif d'une triode et d'un circuit résonnant - voir en a pour un circuit résonnant, c'est-à-dire oscillant non amorti), ce qui est l'exemple le plus classique de relation courant - tension de forme non linéaire. Il est décrit par l'équation:
|
|
|
On montre que ce système admet une bifurcation menant à un cycle limite. Ce phénomène est connu en électronique sous le nom d'auto-excitation. |
|
L'équation différentielle de l'applet de Lucien Dujardin est de la forme: q" + e ((q/q0)2 - b) q' + q = 0 Deux
applets
identiques
sont
affichées
pour pouvoir
comparer les
trajectoires
avec des
paramètres
différents. |
||
|
|
||||
|
|
|
|
|
EN COURS |
|||||
|
L'idée
neuve de
René
Thom est
d'appliquer
à la
topologie le
théorème
de Morse («
on peut
approcher
toute fonction
numérique
de classe Cm
à n
variables par
des fonctions
dont les
points
isolés
sont des
points
critiques (la
dérive
s'annule en
ces points) et
pour lesquels
la
dérivée
seconde est
une forme
bilinéaire
associée
à une
forme
quadratique
non
dégénérée»)
qui devient la
raison
profonde de la
stabilité
de la
singularité
représentée
par le cycle
limite. |
|
Extrait de Thom, 1968f4;p 9-10, (Topologie et signification, 1968, 4. L'Age de la Science, 4, 1968. Réédité comme chapitre 10 in MMM1, 1974, p. 193-228. Réédité comme section 2 du chapitre 10 in MMM2,1980, p. 167-192) |
|||
|
|
Expliquons
notre
modèle
sur un exemple
simple, celui
de
l'oscillateur
linéaire
: L'axe
Oq est
notre espace
substrat E
(on dira aussi
espace
externe).
dont
les
trajectoires
sont les
cercles H
= p2
+ q2
= R2
centrés
à
l'origine. |
|
C'est finalement la nature algébrique de la singularité qui assure l'unité et la stabilité du phénomène vibratoire, au milieu des perturbations incessantes dues à l'univers qui l'entoure. Et c'est ici que nous retrouvons Héraclite ; la physique actuelle nous offre une vision du monde tout à fait compatible avec le panta rei, le mobilisme universel : l'Univers n'est qu'une bouillie d'électrons, de protons, de photons..., etc., tous êtres à propriétés mal définies en perpétuelle interaction. Comment cette bouillie peut-elle s'organiser, à notre échelle, en un monde relativement stable et cohérent, bien loin du chaos quantique et mécaniste que la théorie nous suggère ? Bien que certains physiciens prétendent que l'ordre de notre monde est une conséquence inéluctable du désordre élémentaire, ils sont encore bien loin de pouvoir nous fournir une explication satisfaisante de la stabilité des objets usuels et de leurs propriétés qualitatives. (Comment le pourraient-ils d'ailleurs, alors que les fondements mêmes de leur théorie sont si mal assurés ?) Je crois qu'à cet égard un certain renversement d'optique est nécessaire ; il est illusoire de vouloir expliquer la stabilité d'une forme par l'interaction d'êtres plus élémentaires en lesquels on la décomposerait : comme pour notre oscillateur linéaire de tout à l'heure, la stabilité d'une forme, ainsi que d'un tourbillon dans le flot héraclitéen de l'écoulement universel, repose en définitive sur une structure de caractère algébrico-géométrique (comme la singularité quadratique H = p2 + q2 ), dotée de la propriété de stabilité structurelle vis-à-vis des perturbations incessantes qui l'affectent. C'est cette entité algébrico-topologique que nous proposons d'appeler - en souvenir d'Héraclite - le logos de la forme.» |
||
|
|
|
||||
|
|
Pour
illustrer
pédagogiquement
cette notion
on peut
prendre un
exemple: |
|
On peut maintenant s'intéresser non plus aux dynamiques continues mais aux changements entre dynamiques: aux discontinuités (ou singularités); par exemple dans le cas de l'oscillateur linéaire à caractéristique modulable. |
||
|
3.3 Les singularités, point de concentration de la dynamique sous-jacente (qui peut être redéployée à partir d'eux dans des cas simples) |
|||||
|
EN JACHÈRE 2007 |
|
Vers une typologie des régulations, René Thom, 1985, 5. In Concepts and Formalizations in the Control of Breathing, J. Demongeot et al. (eds.), Manchester University Press, 1987. Voir article "Thermodynamique: processus irréversibles non linéaires": modèle de la glycolyse et de l'agglutination des acrasiales Dictyostelum ...modèle de Chemostat de Monod et Szilàrd présenté par L. Dujardin. |
|
Extrait de Prédire n'est pas expliquer, René Thom, 1991, Eshel, Paris, dans la collection «La Question» dirigée par Émile Noël; « Mais les singularités apparaissent lorsque l'on soumet en quelque sorte l'espace à une contrainte. La manche de ma veste, si je la comprime, je fais apparaître des plis. C'est une situation générale. Cela ne relève pas de la mécanique des matériaux. J'énonce en réalité un théorème abstrait : lorsqu'un espace est soumis à une contrainte, c'est-à-dire lorsqu'on le projette sur quelque chose de plus petit que sa propre dimension, il accepte la contrainte, sauf en un certain nombre de points où il concentre, si l'on peut dire, toute son individualité première. Et c'est dans la présence de ces singularités que se fait la résistance. Le concept de singularité, c'est le moyen de subsumer en un point toute une structure globale.» |
|
|
|
|||||
|
Quelques différences entre la Théorie des catastrophes et les statistiques |
|
|
|
|
|
|
|
|||||
|
on associe à un nuage des points expérimentaux (x,y,...; u,v,...) des fonctions lisses de variables réelles les plus simples possibles F(x,y...,u,v...) |
|
on associe à un nuage de points expérimentaux (y,x) une fonction de distribution (droite de régression, courbe de Gauss, fonction exponentielle, aire....) le lien entre y et x n'est défini que dans l'espace d'observation mais on ignore totalement le lien entre les paramètres dans un autre espace... |
|||
|
|
|||||
|
|
|
|
|||
|
avec les mots de René Thom (Paraboles et Catastrophes, p 82) « toute statistique amène évidemment à un nuage de points mais les espaces où sont placés ces points n'ont pas de groupes d'équivalence qui agissent d'une manière transitive en chaque point comme le groupe euclidien dans l'espace ordinaire. Les variables de contrôle ont souvent une nature ontologique radicalement différente.» ou encore (p 85, en faisant référence à la caverne de Platon) « la théorie des catastrophes suppose (...) que les choses que nous voyons sont seulement des reflets et que pour arriver à l'être lui-même il faut multiplier l'espace substrat par un espace auxiliaire et définir dans cet espace produit l'être le plus simple qui donne par projection son origine à la morphologie observée.» retour texte |
|||||
|
|
|||||
|
(d'après EU - des applets intéressantes sur les phénomènes chaotiques sont proposées dans la version 10) |
|
D'une façon intuitive le chaos se réfère à toute phénoménologie indescriptible. René Thom n'est pas le dernier à critiquer l'emploi un peu trop fréquent du mot chaotique dans un sens très différent du précédent et qui pourrait s'énoncer comme étant un "comportement" qui se caractérise par une "divergence des orbites dans l'espace des phases". Lorsqu'il apparaît dans un système habituellement à l'équilibre on parle de sensibilité aux conditions initiales (SCI). David Ruelle et Floris Takens ont montré en 1971 que la dépendance aux conditions initiales ne pouvait apparaître que dans un système dynamique ayant au minimum trois fréquences indépendantes (ce qui revenait à dire trois variables ou trois degrés de liberté). |
|
En effet, dans un espace à deux dimensions, cette divergence entraînerait soit l'extension des trajectoires à l'infini, soit leur recoupement (ce qui ne peut avoir lieu, dans le premier cas, parce que les valeurs prises par les variables restent bornées et, dans le second cas, parce que la nature déterministe du phénomène interdit que les trajectoires se croisent). Il faut donc au minimum un espace de variables à trois dimensions pour que les trajectoires puissent diverger sans exploser à l'infini ou se couper. Assimilant le nombre de variables indépendantes à celui du nombre de degrés de liberté, on arrive à la conclusion qu'un système dynamique non linéaire ayant au minimum trois degrés de liberté peut devenir chaotique. L'exemple le plus simple est celui du pendule ou de l'oscillateur forcé par un « champ » périodique extérieur. |
|
|
|
Imaginons, en effet, un pendule non linéaire entretenu en oscillation à sa fréquence propre f1 ; c'est un système à deux degrés de liberté : position et vitesse. S'il reste isolé, il ne peut devenir chaotique. Influençons son mouvement de manière périodique, par exemple en soumettant son axe à une oscillation de fréquence f2. Le système devient bipériodique (on dit aussi quasi périodique) mais, surtout, il a acquis un troisième degré de liberté: la phase de l'oscillation extérieure. C'est un fait que le système peut, maintenant, devenir chaotique et, en effet, pour certaines valeurs de l'amplitude du forçage extérieur, des mouvements désordonnés apparaissent. |
||||
|
|
|||||