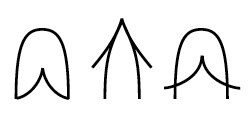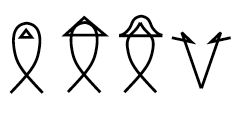Conférence donnée à Poitiers
(Palais des congrès) le 8 octobre 2005 à
20h30
Les diapositives sont sur fond de couleur crème,
les commentaires oraux ont été
résumés (ou complétés) en vert et en
italique et placés entre les diapositives.
Certains documents manquent étant
donné que leur publication sur internet n'est pas possible
pour des raisons de droits d'auteur. Des liens sont
établis avec les autres pages du site de l'auteur.
Être professeur-chercheur au
lycée
Pierre STOUFF, professeur agrégé
Lycée Pierre Guéguin, Concarneau (29)
|
Cet titre a été
donné un peu vite en juin même s'il reflète une
des idées présentées. Je crois qu'il serait
préférable de le modifier...
|
Susciter des vocations de
chercheurs au lycée
Pierre STOUFF, professeur
agrégé
Lycée Pierre Guéguin,
Concarneau (29)
|
|
« Dans l'ensemble je crois qu'on
sait trop de choses en Biologie contemporaine, sans
qu'on sache faire le tri entre ce qui est important et
ce qui ne l'est pas. Il faudra bien revenir un jour
à des théories plus grossières,mais
fondées sur l'essentiel (i.e. sur le
système minimum de contraintes que doit
satisfaire l'être vivant). Peut-être ce jour
est-il moins lointain qu'on ne le croirait.» (Thom,
lettre dans 1987i.pdf p 14)

(Photo extraite du CDRom des Œuvres
complètes de René Thom publié par
l'IHES: http://www.ihes.fr/~cdthom/)
|
Je vis de la biologie.
J'ai souvent dit à mes élèves que je vivais de
la biologie et j'ai retrouvé chez Thom cette même phrase
( 1990f1_4.pdf, p 8; «
Dans ma propre écriture, je mêle de manière quasi
indissoluble la pensée verbale et l'idéalité
mathématique. Cela ne va pas sans inconvénient. Ce
style mixte irrite le mathématicien professionnel,
habitué à traiter mathématiquement l'être
mathématique ; et déconcerte le
non-géomètre (...) à qui la face
mathématique de ma pensée échappe
irrémédiablement. Mais je vis de ce
contact, et si ma pensée a quelque valeur, c'est
de
cette symbiose qu'elle la tire. La pensée purement
mathématique, quand elle est formalisée, est aveugle,
mais capable de marcher, et même fort loin. La pensée
intuitive, au contact du réel, est le paralytique de la
parabole, qui voit, mais ne peut pas progresser
sûrement». ).
Résumé:
Des modèles implicites font partie de l'imaginaire de
l'enseignant avant de faire partie de celui des élèves.
Le premier conseil est d'expliciter les modèles
employés. Un nouveau modèle de cellule se dessine avec
pour traits : le rôle central et structurant de l'eau,
l'importance des changements de phase ou encore la chimie
orientée des complexes structurés.
|
Quel modèle de cellule en lycée
?
|
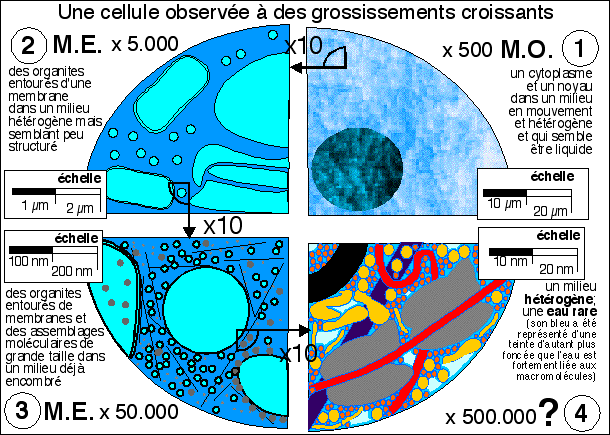
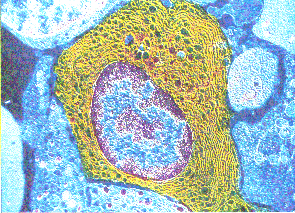
Cellule eucaryote
observée au MET, recolorée
artificiellement (x9 500).
La cellule eucaryote est
caractérisée par un noyau qui
«enferme»
le matériel génétique et un
cytoplasme qui réunit un dédale de
vésicules, sacs, cavités... limités
par une membrane, de nombreux organites à
« double membrane »
(mitochondries...) et des agrégats
moléculaires, le tout
«baignant» dans une sorte de
gelée plus ou moins liquide,
le cytosol.
La cellule eucaryote
apparaît ainsi comme une structure compartimentée,
ce qui permet de séparer dans l'espace et
dans le temps les différentes
réactions chimiques qui
caractérisent la vie. Tous ces
compartiments communiquent cependant entre eux,
faisant de la cellule un ensemble fonctionnel
cohérent.
|
Nathan, spécialité TS, p 50 (image
à résolution fortement diminuée)
|
- le microscope optique (M.O.
- 1) ne permet guère que de
voir le noyau et le cytoplasme dont le contenu nous paraît clair
mais hétérogène (un peu grumeleux). On peut aussi
entr'apercevoir de gros organites comme des vacuoles, des
chloroplastes ou des mitochondries. On peut colorer la cellule sans la
tuer et voir par exemple les chloroplastes se déplacer
entraînés par les mouvements du cytoplasme.
- Au microscope électronique (M.E.
2 et 3) la cellule est morte et
fixée. Les structures ne sont pas vivantes mais mortes. De
plus, on ne voit que celles qui fixent le colorant utilisé
(tétroxyde d'osmium). On observe cependant une grande
variété de structures. En 2
on distingue des mitochondries, des vésicules et les citernes
du réticulum. En 3
les plus gros assemblages protéiques apparaissent comme les
ribosomes et les microfilaments du cytosquelette.
- L'étape 4
n'est pas vraiment accessible à la microscopie pour des
structures complexes en place mais représente ce que l'on
peut imaginer être la réalité à partir
d'observations de quelques éléments réellement
observés mais isolés de la cellule et d'autres
structures. On reconnaîtra en partant du coin gauche et en se
déplaçant en diagonale vers le bas à droite: une
vésicule dont la membrane (en noir) est une structure de
près de 8 nm d'épaisseur, des macromolécules (en
jaune) avec leur(s) couche(s) d'eau interfaciale (les plus grosses
protéines globulaires atteignent typiquement 5 nm de
diamètre), un microfilament fin dessiné en
arrière plan (en violet, leur diamètre varie de 5 nm
pour les plus fins à 25 nm pour les plus épais), deux
ribosomes (en gris, de diamètre environ 20 nm) autour d'un ARNm
(en rouge, un filament de diamètre inférieur à 2
nm qui est le diamètre de la molécule d'ADN); les
molécules organiques plus petites (de diamètre voisin du
nanomètre - pensez qu'un aa comme la phénylalanine
atteint déjà le nanomètre si l'on tient compte de
sa couche d'eau interfaciale - voir plus bas) avec leur(s) couche(s)
d'eau interfaciale encombrent le hyaloplasme; l'eau "libre" (en bleu
clair) est rare et concentrée dans certains espaces.
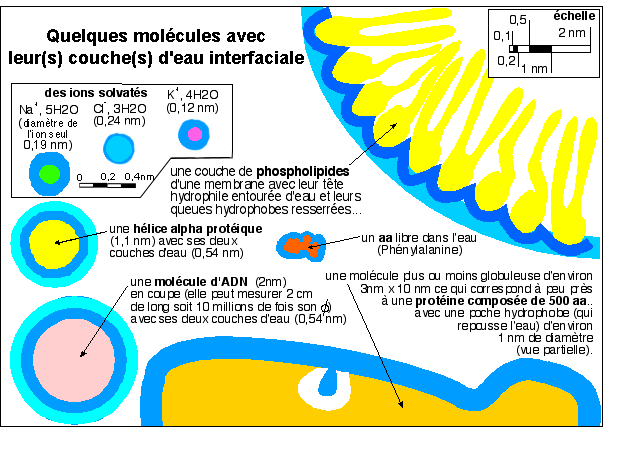
Même si les spécialistes
discutent pour savoir quel est le nombre habituel de couches d'eau
interfaciale (hydratation shell) autour des macromolécules,
elles sont omniprésentes. Une molécule est toujours
entourée d'eau plus ou moins fortement attachée
à elle. Cette eau est ordonnée selon les interactions
qu'elle développe avec la molécule à laquelle
elle se lie: on parle aussi d'eau liée ou d'eau
structurée. Par rapport à la figure 1, cette figure
correspondrait à un grossissement environ dix fois plus fort
le grossissement le plus fort de la figure 1 soit environ 5.000.000
de fois; ce qui n'est bien sûr pas accessible à une
quelconque technique microscopique sur des molécules en place
dans un cytoplasme, et encore moins sur de la matière vivante.
Nous devons donc nous contenter d'interprétations,
réalisées par des méthodes indirectes, et non
d'observations. Il est important de signaler que cette eau
interfaciale est en perpétuel turn-over avec l'eau
environnante, les temps de résidence de l'eau (dans le
milieu interfacial) variant en fonction du groupement auquel elle est
associé (très court pour des groupements
ionisés, beaucoup plus long pour des groupes
hydrophobes).
|
Vers un nouveau modèle
L'eau représente près de 80%
en masse de la cellule vivante mais cette eau est à
près de 80% sous forme d'un film interfacial
d'environ 1,1 nm d'épaisseur qui se trouve entre les
molécules organiques structurant la cellule. Il reste
donc 20% d'eau libre où s'appliquent les lois de la
chimie des solutions aqueuses.
|
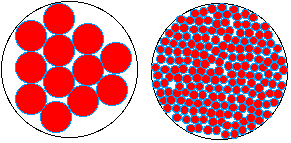
V =
70 µm3
|
|
|
100 sphères
d'1µm de Ø
V eau
interfaciale = 0,25% V
|
|
73 millions de
sphères de 10 nm de Ø
V
eau interfaciale = 20% V
|
La cellule est une
sphère structurée dont la cohérence
vient de son eau interfaciale qui lie les composants entre
eux.
|
À la suite de certaines interventions
lors du symposium "Curvature and Energy in Biology : The
language of Shape", notamment la conférence de
Ninham
Barry "The present
state of molecular forces in colloid science and biological
systems", qui se sont tenues le lendemain de ma
conférence, je tiens à modifier
légèrement mes propos : les physiciens se sont bien
évidemment emparés de la cellule et certains d'entre
eux commencent à proposer de nouvelles formulations concernant
les forces présentes dans le cytoplasme vivant. Ces
idées ne sont pas vulgarisées (à ma
connaissance); Ninham parle d'un " véritable zoo de
nouvelles forces proposées". La cohérence des
composants cellulaires peut bien évidemment s'exprimer au
moyen de la notion de forces ou d'interactions.
|
|
Albert Dacq, un des pères de
l'embryologie expérimentale, travaille en
1832 sur l'œuf vierge d'Ascidie (Tuniciers):
|
|
«...
cette goutte de protoplasme fluide (...) est
limitée par un film cortical plutôt
que par une membrane. Aussi la moindre
éraillure de ce film provoque-t-elle une
cytolyse noire qui s'étend en une
fraction de seconde à l'ensemble du corps
cellulaire. (...) Insistons sur la
fluidité du plasma de l'œuf vierge.
Elle se constate à toutes les phases de
la section et ressort à la fois du mode
de déformation et de la tendance au
refusionnement (...) L'état de sol du
cytoplasme de l'œuf vierge est
aisément modifiable: les chocs, la
pression, le roulage de l'œuf sous
l'aiguille provoquent une gélification
progressive du cytoplasme. C'est ainsi
qu'après avoir opéré une
section, il est extrêmement difficile de
diviser de nouveau l'un des fragments. Je n'ai
pu y parvenir que deux fois. Lors de la seconde
section, le film cortical ne se déprimait
plus, l'aiguille pénétrait dans le
cytoplasme comme dans un bloc de gélatine
et la cytolyse envahissait la tranche vive ainsi
formée. La fécondation
paraît agir dans le même sens, car
la différence de consistance entre
l'œuf fécondé et l'œuf
vierge est frappante. Pendant les 10 minutes qui
suivent la fécondation, la section reste
possible, mais après cette période
elle devient irréalisable. L'aiguille ne
déprimant plus le cortex, elle y creuse
une tranchée, et coupe l'œuf comme
un fruit. (...) La cinèse de segmentation
se produit dans un cytoplasme plus ou moins
gélifié ».
|
|
|

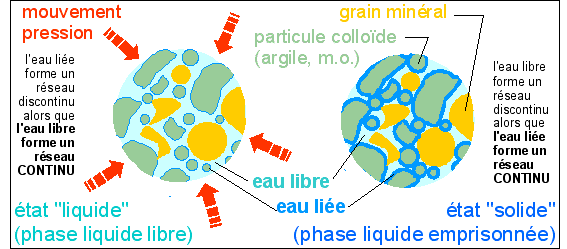
"Sables mouvants" (boues ou vases
thyxotropiques) ;
l'eau liée est représentée à
l'extérieur mais peut être à
l'intérieur et faire gonfler les particules de
colloïdes.
Le cytoplasme est doué de
thyxotropie.
|
|
|
....
film
|
Le principe des "pinces" de
type "laser tweezers"
|
|
La fluidité
membranaire d'un neurone mise en évidence
avec la technique des pinces "laser tweezers".
|
....
film
|
|
Les films avaient été extraits
du CDRom accompagnant la nouvelle édition de Biologie
Moléculaire de la Cellule (Alberts et al.,
Médecine-sciences, Flammarion, 2005)
On étire la limite cellulaire SANS
RUPTURE (sans discontinuité). Je peux vous soumettre deux
explications:
* La première fait appel à un imaginaire très
habituel des forces moléculaires des composants membranaires
(c'est la voie réductionniste). Mais avec ce que l'on
vient de voir sur l'eau interfaciale dans la cellule il est difficile
de soutenir que la membrane est élastique alors
que l'on sait qu'elle est fluide.
* La seconde est beaucoup plus inhabituelle (c'est la voie
structurale) et repose sur la morphologie (je précise que
mon explication reste très imparfaite car je n'ai pas les
conditions précises de l'expérience). La cellule
nerveuse étirée présente déjà une
morphologie dendritique: un corps cellulaire avec de
nombreux prolongements stabilisés par un dynamique interne que
l'on pourrait appeler métabolique. La membrane est le bord de
la cellule, c'est un surface de discontinuité qui est
stabilisée par les fonctions du vivant et donc par la
dynamique métabolique. On doit cette vision à
René Thom. Si l'on peut déformer sans rupture la limite
cellulaire c'est que cette forme reste compatible avec la forme
stable de la cellule.
Avant d'essayer d'expliquer cette vision je fais la remarque qu'il y
a plusieurs corollaires évidents à cette
hypothèse; en voici deux :
- on devrait pouvoir induire la formation de dendrites par d'autres
mécanismes que la pince laser, comme par exemple une
modification chimique du métabolisme; ce qui pourrait
être le cas lorsque certains contacts synaptiques sont
déduits et que de nouveaux dendrites croissent même chez
des cellules nerveuses âgées (ce sont des cas de
neuroplasticité).
- pour une cellule de forme stable sphérique (par exemple un
ovocyte) on ne devrait pas pouvoir déformer stablement la
cellule. Les expériences d'injection ou d'excision de noyau de
l'ovocyte montrent que la membrane peut être percée et
écartée et que la forme sphérique reste stable.
Toujours dans la même source documentaire il y a un petit film
sur l'hématie:
|
|
....
film
|
Cellules embryonnaires
nerveuses de l'hippocampe d'un Rongeur. Les
prolongements fins (neurites) naissent à
partir de cônes de croissance.
|
|
Déformation aux pinces
laser tweezers d'une hématie puis lyse dans
une solution saline.
|
....
film
|
|
|
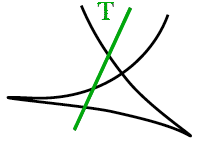
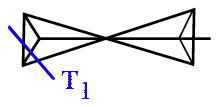
Prédire n'est pas expliquer, René Thom, 1991,
Eshel, Paris, dans la collection «La Question»
dirigée par Émile Noël;
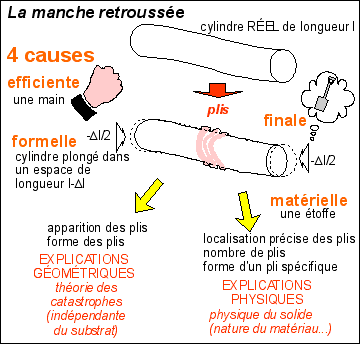
« Mais les singularités
apparaissent lorsque l'on soumet en quelque sorte l'espace
à une contrainte. La manche de ma veste, si je la
comprime, je fais apparaître des plis. C'est une
situation générale. Cela ne relève
pas de la mécanique des matériaux.
J'énonce en réalité un
théorème abstrait : lorsqu'un espace est
soumis à une contrainte, c'est-à-dire
lorsqu'on le projette sur quelque chose de plus petit que
sa propre dimension, il accepte la contrainte, sauf en un
certain nombre de points où il concentre, si l'on
peut dire, toute son individualité première.
Et c'est dans la présence de ces
singularités que se fait la résistance. Le
concept de singularité, c'est le moyen de subsumer
en un point toute une structure globale.»
|
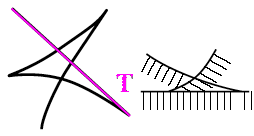
voie structurale
les points des plis forment un
ensemble (ce que l'on appelle un
"fermé") de points
catastrophe ou
une catastrophe qui s'opposent aux points
réguliers (non pliés) de la
manche qui forment un "ouvert".
|
|
voie
réductionniste
|
|
Pour des précisions sur l'utilisation
en science des 4 causes présentées pat Aristote, voir
une page sur ce
site.
|
Un exemple de modèle
interne (métabolique) structural
|

|
Un bourgeonnement
....
c'est comme un pli (au niveau
d'une manche) avec une symétrie
sphérique et non plus cylindrique
|
René Thom, 1968 (Stabilité structurelle et
morphogenèse; essai d'une théorie
générale des modèles, stabilité.pdf,
p 326)
« Dans un milieu extérieur E
où règne un flux continu d'énergie en
voie de dégradation thermique, on suppose
donnée une boule B de rayon r, où règne
un régime dynamique local g consommateur
d'énergie. Admettons que la consommation
d'énergie soit proportionnelle au volume ; la capture
d'énergie, provenant des échanges avec le
milieu extérieur, n'est alors proportionnelle
qu'à la surface. Si le rayon r est au départ
assez petit, il y aura excès de l'énergie
capturée sur l'énergie consommée ; on
admettra que cet excès d'énergie est
consacré à la synthèse de substances
support du régime g, de sorte que le volume V (donc
le rayon r) ira croissant. Si ce processus de croissance
était rigoureusement proportionnel à
l'accroissement d'énergie, le rayon r irait en
croissant asymptotiquement vers un rayon r0, valeur
d'équilibre pour laquelle l'énergie
capturée est égale à l'énergie
consommée. Supposons alors que ce mécanisme de
synthèse présente une certaine inertie, un
certain retard. Il pourra alors y avoir accroissement du
volume au-delà du volume optimal, au détriment
de la consommation d'énergie interne ; la boule, de
régime g et de rayon r > r0 entre alors dans un
état d'instabilité dont elle ne pourra sortir
que par cassure ; après fragmentation en deux boules
de petit rayon r1, plus petit que r0, la croissance pourra
reprendre, suivie de multiplication ».
|
|
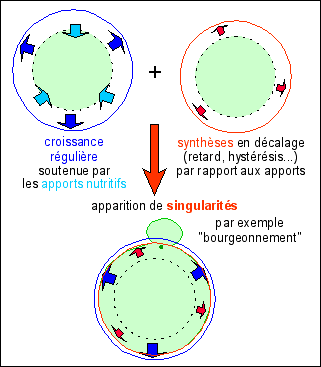
Les formes naturelles peuvent, à
condition de poser quelques hypothèses acceptables
simples, être modélisées à
partir de conflits de dynamiques stables
(représentées mathématiquement par
des attracteurs).
|
Cette explication est clairement
structurale. La forme est ici une boule. La dynamique un
accroissement de volume isotrope sous-tendu par une dynamique
biochimique (entrées de matière "brute",
dégradation et synthèses de composés).
L'instabilité conduisant à la catastrophe mitose est
due à un décalage (retard, hystérésis,
hétérochronie...) entre énergie nutritive
entrante (que l'on suppose stable) et les
synthèses.
Pour des explications sur la
théorie des catastrophes plusieurs pages sont disponibles sur
internet: un article
d'Ivar
Ekeland paru dans
La Recherche, une page
générale
sur la théorie des modèles de
René Thom et des
pages complémentaires plus mathématiques mais faites
pour des étudiants en biologie avec des applets java et des
petits modèles dynamiques. Il est hors de question de
présenter cette théorie ici il nous suffit de savoir
que c'est un générateur de modèles de toutes les
formes naturelles biologiques (et non biologiques!).
|
Reformulation d'une idée
déjà ancienne sur les systèmes
orientés ou finalistes
modèle "soupe"
chaîne métabolique statistique
|
modèle "machinerie haute
technologie"
chaîne métabolique finaliste
|
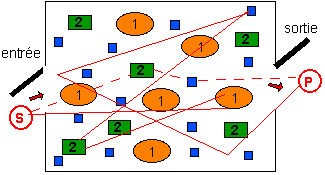
système métabolique statistiquement
homogène compris comme
- un ensemble statistiquement
déterminé de
molécules en solution aqueuse (non
dénombrables) dont le comportement
dépend des:
- concentrations (et donc d'une
répartition supposée statistiquement
homogène) des espèces en solution et de
- réactions à l'équilibre
(et donc une vitesse moyenne (statistique) de
réaction dépendant des paramètres
physiques et des concentrations...).
|
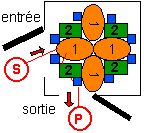
système métabolique
hétérogène composé
de:
- molécules dénombrables (tant
de molécules de telle enzyme, tant de
molécules de telle autre enzyme) et donc
considérées comme des molécules
individuelles, à un emplacement donné
(environnement particulier), avec une fonction
donnée et des paramètres individuels
(qui peuvent varier selon les molécules)
- ayant un mobile commun
déterminé par UN SEUL CHEMIN possible
(ou quelques-uns) pour aller du point d'entrée
au point de sortie ("mobile" au sens
étymologique (mécanique) de rouage pris
ici selon son sens analogique dérivé de
fin).
|
La stabilité du
système vient de la dynamique (et
donc par exemple de la fonction de nutrition) et
non de propriétés intrinsèques aux
molécules.
|
|
Les dynamiques stables ? Des fonctions
globales qui caractérisent le vivant.
La vie est un travail :
Il y a 3 grandes fonctions ou fonctions non
locales qui caractérisent le vivant:
Le travail
de nutrition comprend
l'ensemble des phénomènes de prise ou de rejet
de matière et d'énergie vis-à-vis du
milieu extérieur et qui permettent à
l'organisme de se maintenir en vie (alimentation, digestion,
respiration, circulation,excrétion ...). Les autotrophes
(du grec "auto" = "soi-même" et
"trophé"= "nourriture") se
nourrissent seuls sans dépendre d'autres êtres
vivants. Les hétérotrophes ou plutôt allotrophes
(du grec "hétéro" = "l'autre, en tant que
différent" et du grec "allo"= "l'autre, en tant qu'un
autre que moi") consomment d'autres
organismes vivants ou morts qui sont les proies.
Le travail
de reproduction correspond
à la capacité des êtres vivants de se
multiplier. La reproduction peut être asexuée
(solitaire) ou sexuée (entre deux organismes de sexe
opposé).
Le travail
de relation correspond aux
communications entre l'organisme et son milieu
(écosystème) ou entre les différentes
cellules d'un organisme.
|
Voir compléments sur
la cellule (modèle
soupe/machinerie haute technologie) et La
vie
est un travail.
|
Qu'est-ce qu'une cellule ?
La cellule est une unité
de structure et une unité
de fonction.
Un solide cohérent à la fois
structuré et doué de thyxotropie grâce
à l'eau interfaciale des composants
moléculaires du cytosol.
Une unité au travail dont la dynamique
est caractérisée par des fonctions stables de
nutrition, de relation et de reproduction.
|
|
Qu'est-ce qu'un modèle ?
Une image (mentale ou
concrète) de la réalité qui puisse
être questionnée (pour fonctionner).
|
Statut ontologique:
loi analogique
|
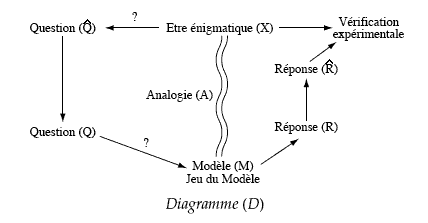
|
Statut
épistémologique:
questionnable, fournit une
réponse à une question
|
La vérité du modèle
est dans l'analogie (justification a priori);
son efficacité pragmatique dans sa
capacité prédictive et
compréhensive (justification a
posteriori).
|
« ce qui est important dans un
modèle, ce n'est pas son accord avec
l'expérience, mais au contraire sa «
portée ontologique . (…) En effet,
étant donnée n'importe quelle morphologie
empirique, il est toujours possible d'exhiber un
modèle quantitatif - contenant suffisamment de
paramètres arbitraires - , qui rendent compte de
l'expérience à une approximation
donnée. Si l'on veut avoir un bon modèle, il
faut éliminer au maximum ces paramètres
arbitraires » (René Thom, 1971, Modèles
Mathématiques de la Morphogénèse;
p 106)
René Thom, 1968, Stabilité Structurelle et
Morphogénèse : Essai d'une théorie
générale des modèles.
|
|
Un écueil: faire jouer le modèle sans
question;
Un constat de manque d'ambition: le trop fort
degré d'analogie entre les modèles et les
êtres réels ce qui diminue leur valeur que Thom
chiffre au rapport entre les gains (efficacité) et le
niveau du pari (niveau d'analogie).
Expliciter les modèles :
de la technique à
l'art* des modèles
|
- préciser l'analogie :
|
|
... la cellule vivante est
comparée à un tube à
essais compartimenté avec des
composés en solution aqueuse et dans
lequel agit la loi d'action de masse...
|
// |
... la cellule vivante est un
système dynamique stable par ses
fonctions globales (nutrition, relation,
reproduction); les dynamiques locales sont
exprimée par des conflits ou des
bifurcations d'attracteurs dans un espace
métabolique de grande dimension...
|
|
- préciser les
questions :
|
|
Dans le modèle
génétique moléculaire, la
recherche d'une séquence d'ADN chez un
individu se fait-elle pour conforter l'analogie
ou y-a-t-il vraiment une question posée
AU MODÈLE ?
|
* «… ce
que nous apportons ici, c'est non pas une théorie
scientifique, mais bien une méthode ; décrire
les modèles dynamiques compatibles avec une
morphologie empiriquement donnée, tel est le premier
pas dans la construction d'un modèle ; c'est aussi le
premier pas dans la compréhension des
phénomènes étudiés. De ce point
de vue, nos méthodes, trop
indéterminées en elles mêmes, conduiront
à un art des modèles et non à une
technique standard explicitée une fois pour toutes
». (SSM, 13.8 B)
|
Résumé: En enseignant que
la forme des protéines dépend avant tout de leur
séquence primaire on emprunte souvent la voie
"réductionniste" d'un déterminisme physico-chimique.
Implicitement, on pousse l'élève à
étendre le modèle qu'on lui a donné pour les
enzymes à toutes les protéines actives. Le
deuxième conseil est alors de dépasser les limites des
programmes, des manuels... en suivant par exemple René Thom,
qui propose une voie "structurale" de compréhension de
l'activité moléculaire. Les activités des
protéines, tant mécaniques qu'électriques ou que
chimiques, sont alors reliées à leur forme mais pas
à une structure tridimensionnelle STABLE. Un embryon de
typologie morphologique peut être esquissé.
|
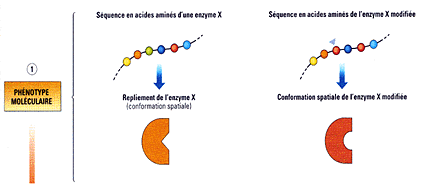
La séquence primaire DÉTERMINE
la conformation spatiale (cause matérielle OUI mais
cause formelle NON).
Belin, 1èreS, 2005, p 137
|
Pour des précisions sur l'utilisation
en science des 4 causes présentées pat Aristote, voir
une page sur ce
site.
|
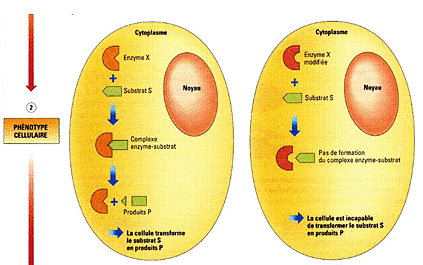
La conformation spatiale DÉTERMINE
l'activité ou la fonction (cause matérielle
OUI, mais formelle et efficiente NON).
Belin, 1èreS, 2005, p 137
|
|
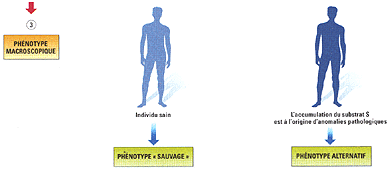
La protéines DÉTERMINENT
toutes les caractéristiques structurelles et
fonctionnelles de l'individu !!!! (cause finale NON).
Raisonnement INVERSE:
La vie repose sur des fonctions stables (travail de
relation, de nutrition, de reproduction); les cellules
sont des unités de structure et de fonction
(locale) de ces fonctions globales; les molécules
sont les traces de ces dynamiques locales.
Belin, 1èreS, 2005, p 137
|
|
Une vision de l'activité
enzymatique (clé-serrure) conforme au programme
du lycée ... et à l'imaginaire de
certains.
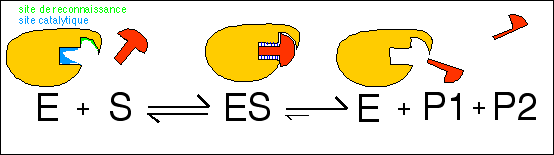
Où
est la vie dans ce modèle ?
|
....
(film Biologie
Moléculaire de la Cellule)
La main ATP-dépendante
|
Comment tourner une
clé dans une serrure sans une main ?
La main (cause efficiente) est placée dans le
"hasard" des mouvements de diffusion ...
Le substrat et l'enzyme ne peuvent pas
être des formes
statiques (un cristal) mais
doivent être des formes
métaboliques
(dynamiques: toutes les formes vivantes).
Vous ne pouvez pas faire interagir deux formes statiques
sans l'intervention d'une forme dynamique. Le cristal de
NaCl se dissous dans l'eau car il présente à
son interface avec le solvant une oscillation permanente
à l'échelle des liaisons atomiques...
Les enzymes et les
substrats DANS LA CELLULE sont des formes
métaboliques.
René Thom, 1968, Stabilité Structurelle et
Morphogénèse : Essai d'une théorie
générale des modèles.
|
|
E + S < = > ES
< = > E + P1 + P2
S' état de transition du substrat
S
< = > (S')
< = > P1 + P2
L'enzyme E possède une
affinité maximale pour S' et non pour S
E + S
< = > ES'
< = > E + P1 + P2
|
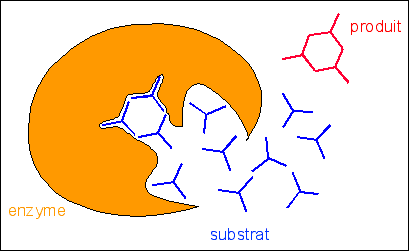
Une forme
"métabolique" encore bien "statique"
|
|
E
+ 3S
< = >
E3S'
< = > E
+ P
D'après Encyclopedia
Universalis, catalyse enzymatique -
illustration de l'article "liaisons
biochimiques faibles"
|
|
|
Approcher les dynamiques
http://pst.chez.tiscali.fr/CT/continud.htm
(paragraphe 3.2c)
|
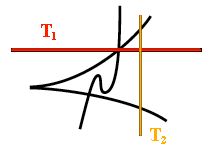
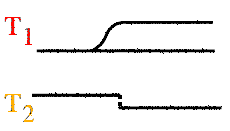
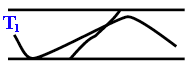
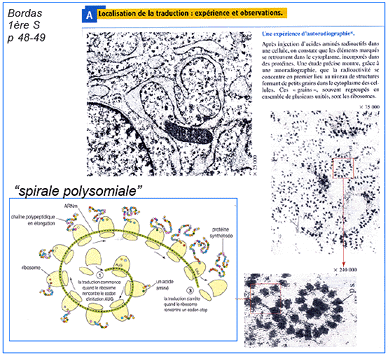
On est tenté d'assimiler le
plan (x,y) des observations au plan (x,t) des
positions, mais cela n'est pas possible car on a
un cadavre fixé et coloré. Les
physiciens utilisent l'espace
des phases*. Pour un
point animé d'un mouvement dans un plan ,
l'espace des phases est un plan (x,v). On pourrait
alors avoir une spirale divergente (ou
convergente) dans le cas d'un système
linéaire amorti. Dans l'espace des
positions on a une trajectoire linéaire
bornée aux deux extrémités,
ce qui n'a rien à voir avec notre
"spirale". Pour obtenir une telle morphologie la
dynamique est donc plus compliquée (deux
attracteurs** au moins doivent s'affronter). Il
faut approfondir ses bases mathématiques et
surtout géométriques et analytiques.
*espace abstrait qui permet de définir
complètement l'état d'un
système à partir de la connaissance
des coordonnées de ce système dans cet
espace
** attracteur; régime asymptotique stable
(atteint au bout d'un temps infini)
|
Seul l'espace des phases
permet d'approcher les dynamiques.
|
|
Exemples de morphologies dans un espace
R4 obtenues à partir de conflits d'attracteurs
René Thom, SSM, Fig
13-18 p 451
|
|
FONCTION: une enzyme pour quoi faire ? ...
couper, lier, accrocher, dupliquer....
STRUCTURE: quelle forme stabilisée par quelle
dynamique stable ? ... nutrition, relation, reproduction.
Une enzyme est une forme
métabolique associée à un substrat,
à ses produits, mais aussi à toute sa
chaîne de synthèse.
L'enzyme n'a de SENS (signification) que dans son contexte
dynamique qui la CAUSE (cause efficiente et formelle; la
cause finale est toujours la vie).
|
classification
internationale des enzymes
(chimique)
|
classification
fonctionnelle topologique
|
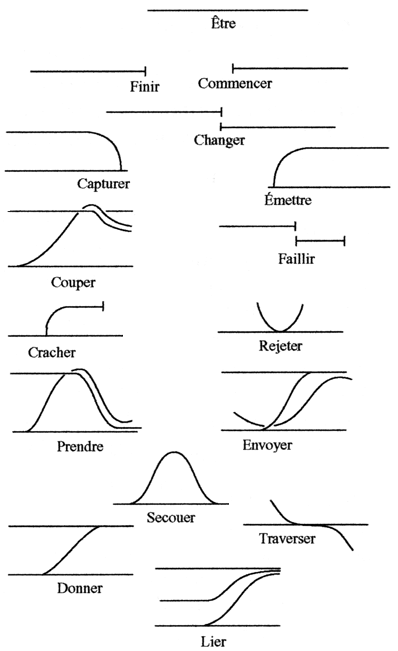
Table des morphologies
archétypales, René Thom, SSM,
Figure 13-18, p 451 ordre modifié
|
types fonctionnels d'enzymes
|
|
n° et nom
|
action vue du côté du bilan chimique
(produits, réactifs, atomes
impliqués, répartition de charges)
|
réversibilité
|
nombre d'acteurs
|
verbes associés
aux morphologies
|
- des enzymes nourricières
qui transfèrent
de la matière ou de
l'énergie...)...capturer
des proies, les assimiler (prendre),
capter la
lumière, capter de l'air, rejeter
des déchets
- des enzymes relationnelles
informatrices qui peuvent envoyer
des signaux, se déformer (changer,
secouer, traverser) en fonction des
signaux reçus, protéger
(chaperonines... par isolement de la structure
à protéger)...
- des enzymes reproductrices
qui réalisent des isomorphismes... comme
une ADNpolymérase (ou plutôt tout
le complexe réplicatif dont l'ADNpol) qui
fabrique une copie d'une molécule...
|
|
1 oxydo - réductases
|
transfert d'e-
|
+
|
2/1*
|
changer
capturer
émettre
|
|
3 hydrolases
|
hydrolyse (transferts de groupements fonctionnels
à l'eau)
|
-
|
1/2**
|
couper
faillir
|
|
4 lyases
|
addition d'un groupement fonctionnel sur une
double liaison ou formation d'une double liaison
par élimination d'un groupement fonctionnel
|
+
|
1/2***
|
cracher
rejeter, prendre, envoyer
|
|
5 isomérases
|
transferts de radicaux à
l'intérieur d'une molécule donnant
une forme isomère
|
+
|
1
|
secouer
|
|
2 transférases
|
transfert de groupements fonctionnels
|
-
|
2
|
donner/
recevoir
traverser
|
|
6 ligases
|
formation de liaisons covalentes C-C, C-S, C-O,
C-N par réaction de condensation
couplée à une hydrolyse de l'ATP
|
-
|
2
|
lier
|
|
* 1 si l'on compte le coenzyme; 2 si l'on ne
considère que le substrat oxydé ou
réduit
** 2 si l'on considère l'eau
*** 2 si l'on considère la molécule
qui donne ou qui reçoit le groupement
fonctionnel
|
|
Pour aller beaucoup plus loin. Je
commence à entr'apercevoir une autre conception des
molécules-fonctions. La matière vivante non pas comme
un ensemble de molécules matérielles à une
certaine concentration et possédant telle ou telle
activité mais bien un ensemble de dynamiques dont les
molécules (et les organites...) sont des structures stables
(ou instables et dans ce cas on ne les voit pas) correspondant
à des conflits de dynamique. Chaque molécule
stabilisée est la trace d'un attracteur. (Voir SSM p 464
extrait ci-dessous).
René Thom distingue les formes
statiques et les formes métaboliques. Pour pouvoir
déclencher une réaction chimique le substrat ou
l'enzyme au moins doivent être une forme
métabolique.
(SSM, 47) «... si E est un espace
topologique, G un groupe (ou un pseudo-groupe) opérant dans E,
une G-forme est par définition, une
classe d'équivalence de fermés de E modulo l'action de
G; Les G-formes ont comme propriété la
stabilité structurelle.
Une G-forme A sera dite structurellement stable,
si toute forme B assez voisine de A dans E est
G-équivalente à A; autrement dit, pour qu'une
classe de G-équivalence F définisse une forme
structurellement stable, il faut et il suffit que la totalité
des points de E de cette classe d'équivalence forme un ouvert
dans l'espace E ». Avec mes mots: un ouvert c'est une boule
sans bord. Un groupe G est un sous-ensemble de E muni d'une loi de
composition interne (associative si c'est un groupe associatif).
C'est à dire que lorsqu'il se passe quelquechose dans E (ce
quelque chose obéissant à la loi définissant le
groupe G) on obtient toujours des groupes équivalents. Cet
ensemble de groupes équivalents par transformation forme un
fermé, c'est-à-dire qu'il a un bord (donc qu'il
présente des discontinuités à ses limites).
Une forme structurellement stable c'est une forme avec un
bord.
Thom (stabilité p 78) présente
deux types de modèles:
Un phénomène naturel, sur
la nature duquel nous ne faisons aucune hypothèse, se
déroule dans une boîte B ; il y aura donc lieu de
considérer le produit B
X
T de B par l'axe des temps T ; ce sera le domaine siège
du processus considéré.
A. Modèle statique
Dans ce modèle, on se donne deux variétés
différentiables M (espace des paramètres internes) et V
(dans la pratique, la variété-but V est le corps
réel ou complexe) ; on admet que le processus peut être
décrit localement autour de chaque point régulier x par
un champ d'applications de la forme G : W
X
M --> V, où W est un voisinage de x dans B
X
T. En chaque point x régulier, l'état local du
processus est décrit par une application g : M --> V = G(x,
m) à partir de laquelle, en théorie, on saurait
exprimer toutes les observables du système.
B. Modèle
métabolique
On se donne, en chaque point x régulier
1. une variété M (espace des paramètres
internes) ;
2. un champ de vecteurs X dans M, dépendant de x ;
3. un attracteur c(x) de la dynamique [M, X(x)].
On admet que X(x) dépend différentiablement de x ; en
fait, seul intervient, pour déterminer l'état local, le
voisinage du champ X(x) au voisinage de l'attracteur c(x) ; le reste
du champ X(x) ne joue qu'un rôle virtuel. Les observables du
système, en particulier, sont déterminées par la
donnée de l'attracteur c(x).
On n'a fait aucune hypothèse sur la classe de
différentiabilité des fonctions g ou X; on les
supposera m fois continûment différentiables, m
suffisamment grand. Un point catastrophique peut être
caractérisé par le fait qu'en ce point, le champ
gx ou c(x) admet une discontinuité ou l'une de ses
dérivées d'ordre ≤ m; en fait, dans les exemples
tirés de la thermodynamique, l'ordre m peut être pris au
plus égal à deux. Il est évident a priori qu'une
discontinuité d'une dérivée de très grand
ordre a toutes chances d'échapper à
l'observation.
C. Évolution des
champs
On admettra qu'autour de tout point régulier x = (y, t), y
appartenant à B, le champ statique ou métabolique voit
son évolution déterminée par une loi
différentielle de la forme
dg/dt = H(g, y, t) (cas
statique)
dX/dt = Hc(x) (X, y, t) (cas
métabolique)
où les opérateurs H
conduisent à des problèmes localement bien posés
; par là on entend, comme d'habitude, qu'il y a existence,
unicité des solutions du problème de Cauchy relatif
à cet opérateur d'évolution et dépendance
continue de cette solution par rapport à la donnée
initiale pour tout un voisinage de cette donnée g(y, 0). On
remarquera que dans le modèle métabolique, la loi
d'évolution dépend de l'attracteur c(x).
(p. 82)
4.4. Champs morphogénétiques associés à
des catastrophes locales
A. Modèles statiques
Nous en arrivons maintenant à la construction fondamentale
qui, à nos yeux, détermine la morphologie d'un
processus à partir de sa dynamique. Considérons d'abord
le cas d'un modèle statique ; soit W l'espace de base (domaine
de l'espace-temps), L(M, V) l'espace fonctionnel fibre. On supposera
qu'il existe un sous-ensemble fermé H du sous-ensemble H de
bifurcation dans L(M, V) qui a la propriété suivante :
soit s : W --> L(M, V) le champ section. On admettra le postulat
essentiel que voici : le processus local ne change
d'apparence phénoménologique qu'en un point où
l'application g : M --> V de la dynamique interne change de type
topologique, de forme. Ainsi, tout point x appartenant
à W tel que s(x) = g soit structurellement stable est un point
régulier du processus.
Tout point catastrophique y est tel que s(y) appartient à
l'ensemble H de bifurcation de l'espace fonctionnel L(M, V). En fait,
dans le seul cas connu de modèle statique, qui est celui
où V est la droite réelle R et qu'on traitera au
chapitre suivant, les régimes stables, attracteurs de la
dynamique locale, correspondent aux minima de g : M --> R; on
obtient alors les points catastrophiques comme contre-images de
strates H de H par s, où H désigne l'ensemble des
fonctions g : M --> R telles que deux minima au moins soient
égaux (convention de Maxwell). Ces strates H admettent souvent
pour bord libre les strates H1 inclus H où deux
minima viennent coïncider ou encore, un minimum se
décompose en deux minima distincts par bifurcation. On
décrira le cas le plus simple de ce phénomène au
chapitre suivant sous le nom de catastrophe de
Riemann-Hugoniot. On résumera l'ensemble de ces
phénomènes par la métaphore ferroviaire :
la bifurcation engendre la catastrophe.
Le modèle statique permet de rendre compte d'un
phénomène important, la propagation des fronts
d'onde et de déterminer théoriquement toutes les
singularités stables des fronts d'onde.
…
C. Modèles métaboliques
Dans un modèle métabolique, ayant pour fibre une
dynamique (M, X) sur W, la théorie se présente ainsi :
dans l'espace fonctionnel F des champs de vecteurs sur X, on a un
sous-ensemble H de bifurcation, ensemble des systèmes au
voisinage desquels la configuration des attracteurs du champ X n'est
pas structurellement stable ; de cet ensemble H, on extrait le
sous-ensemble H' qui donne ceux des champs X pour lesquels
l'attracteur c(x) associé à la section s n'est pas
structurellement stable ; les points catastrophiques du processus
forment alors l'image réciproque par la section s : W --> F
du sous-ensemble H'. Contrairement à ce qui se passait dans le
cas statique, l'ensemble H , bien que (probablement) pourvu d'une
structure stratifiée, n'est pas localement fermé dans F
; de là, peut résulter pour l'ensemble K =
s-1H' une structure topologique compliquée, en
particulier, la présence de points catastrophiques
essentiels.
C'est ce que l'on signifie lorsque l'on
affirme que le substrat présente un état de transition.
C'est la dynamique métabolique du substrat. Quand à
celle de l'enzyme elle semble tout aussi nécessaire puisqu'il
faut bien que réaction chimique se fasse. On a donc deux
dynamiques métaboliques qui entrent en conflit et de la
naît la réaction enzymatique qui aboutit à la
catastrophe "produits + enzyme restituée". L'enzyme ne
différerait des autres molécules de type substrat que
par sa reconstitution en fin de réaction, ce qui en terme de
stabilité nécessite un cycle.
Profonde analogie entre l'outil et l'enzyme.
SSM, p 445 (13.3 Homo faber). L'homme façonne un objet
à l'aide de l'outil en imprimant dans le bloc informe sa
chréode qui préexiste dans son esprit (très
platonicien et très bien accepté chez les
sculpteurs...). De même l'enzyme n'est que la trace de la
dynamique de conflit ou de bifurcation (de la chréode)
sous-jacente. En fait l'enzyme avec sa forme est crée à
chaque fois par la dynamique. C'est pour cela que Thom envisage un
ensemble protéine + ARN + ADN avec la catastrophe filamenteuse
comme trace de la dynamique....Il n'y a pas de matière
synthétisée (en stock dans la cellule) et qui sert ou
non mais bien des dynamiques qui engendrent des molécules
outil fabriquées hic et nunc.
|
|
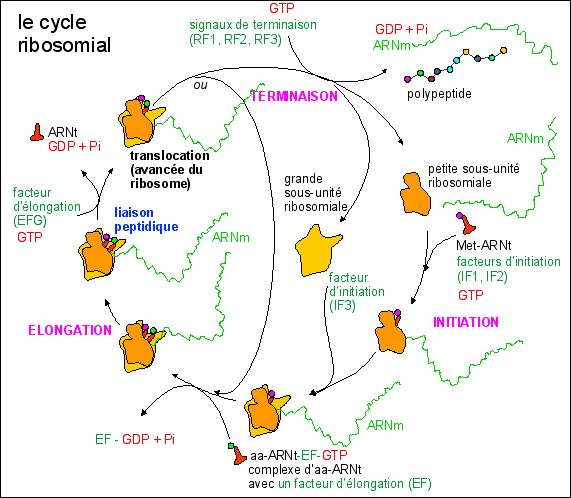
La synthèse des
protéines, une réaction
enzymatique catalysée par les ribosomes,
l'ARNm, les ARNt et de nombreux cofacteurs de
traduction; (chez les Procaryotes
d'après EU)
|
|
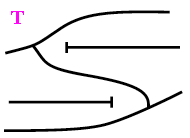
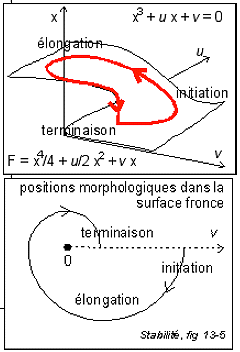
La fronce
Une
représentation de la morphologie de la
dynamique du cycle ribosomial (la surface est le
lieu des points singuliers du potentiel F)
|
n aai
(1,n)+ 4 GTP
< ----------> (Met
+ aai
(2,n-1)+ aan)
+ 4 GDP
+ 4Pi
(enzymes: ARNm,
ribosomes,
ARNt,
cofacteurs)
|
|
La fronce:
Une représentation de la morphologie de la dynamique du cycle
ribosomial (la surface de droite (fronce) est le lieu des points
singuliers du potentiel F, c'est-à-dire le lieu où la
dérivée s'annule, voir page
complémentaire pour
des explications simples avec des exemples)
On notera que la dynamique proposée
est récurrente pour les modèles thomiens
(peut-être parce qu'elle représente un premier niveau
d'approche - qu'il est bien sûr nécessaire de
préciser, ce qui ne peut être fait à ce niveau de
compréhension - ; mon propos ici n'étant que de
souligner l'analogie en me servant d'un outil... que je ne
maîtrise pas mais dont je vois l'utilisation que pourrait en
faire un mathématicien). L'arbre à came de droite
est analogue à la forme des
polysomes dans l'espace cytoplasmique
fixé
et mort. On peut penser que dans ce cas la dynamique
proposée est pertinente et qu'il ne reste qu'à trouver
les paramètres qui ont été figés dans la
coupe. Si le système de synthèse protéique est
stable il n'est pas étonnant que la surface fronce
représente une coupe de l'espace euclidien. Il est urgent de
s'efforcer de trouver des paramètres pertinents de la
dynamique métabolique cytoplasmique. C'est un travail que je
ne peux faire seul. J'en appelle une fois encore à
l'inventivité de notre jeune génération.
On remarquera que l'initiation est habituellement
représentée au centre de la figure mais je ne connais
aucun argument en faveur de cette hypothèse. La dynamique
présentée ici exige que l'initiation se fasse sur le
bord externe du polysome (l'extrémité 5' de l'ARNm avec
sa coiffe ("cap structure") doit se trouver à
cet endroit et non au centre). Je souligne deux points. D'une part,
une dynamique convergente (même si ce n'est pas dans l'espace
euclidien) est plus parlante et conforme à l'intuition (la
libération des sous-unités ribosomiales au point de
potentiel le plus bas permet aisément une
récupération au niveau du site d'initiation voisin).
D'autre part, on peut penser qu'il existe une fonction de
structuration de la protéine au sein du polysome, les
ribosomes pouvant intervenir comme "chaperons". Ceci est une piste de
recherche ouverte (interactions sous-unités ribosomiales -
polypetide en formation). En tout cas la localisation du point
d'initiation devrait pouvoir être assez facilement
précisée expérimentalement.
SSM 13.8 A, p 464
« Résumé des thèses:
1 . Tout objet, ou toute forme physique, peut être
représentée par un attracteur C
d'un système dynamique dans un espace M de variables
internes.
2. Un tel objet ne présente de stabilité, et de ce fait
ne peut être aperçu, que si l'attracteur correspondant
est structurellement stable.
3. Toute création ou destruction de formes, toute
morphogénèse, peut être décrite par la
disparition des attracteurs représentant les formes initiales
et leur remplacement par capture par les attracteurs
représentant les formes finales. Ce processus, appelé
catastrophe, peut être décrit sur
un espace P de variables externes.
4. Tout processus morphologique structurellement stable est
décrit, par une (ou un système de) catastrophe(s)
structurellement stable(s) sur P.
5. Tout processus naturel se décompose en îlots
structurellement stables les chréodes.
L'ensemble des chréodes et la syntaxe multidimensionnelle qui
régit leurs positions respectives constitue un
modèle sémantique.
6. Si l'on considère une chréode C comme un mot de ce
langage multidimensionnel, la signification de ce mot n'est autre que
la topologie globale du (ou des) attracteur(s) associé(s) et
celle des catastrophes qu'ils subissent. En particulier, pour un
attracteur donné, la signification est définie par la
géométrie de son domaine d'existence sur P et la
topologie des catastrophes de régulation qui limitent ce
domaine.
Il en résulte que la signification
d'une forme C ne se manifeste que par les catastrophes où elle
est créée ou détruite. On retrouve ainsi
l'axiome cher aux linguistes de l'école formaliste, selon
lequel la signification
d'un mot n'est rien de plus que l'usage de ce
mot. (Et aussi l'axiome de
l'école des physiciens dite du Bootstrap,
selon lequel une
particule est entièrement définie par le réseau
d'interactions auxquelles elle
participe)».
Cette dernière phrase est
particulièrement intéressante à appliquer aux
enzymes. Une molécule "vivante" est entièrement
définie par le réseau d'interactions auquel elle
participe et dont elle est issue....
|
Le rêve...d'une
dialectique.
dialegein = dia-legein =
à travers - Logos (forme et sens)
Toute protéine, toute
structure cellulaire...
toute forme, toute matière VIVANTE ...
résulte d'une dynamique stable du fait du travail du
vivant qui imprègne tout l'être vivant.
La stabilité des dynamiques est
géométrique.
La fonction enzymatique est une fonction
topologique au sens non pas de la seule
complémentarité "site actif - état de
transition du substrat" sous contrôle de l'environnement
(eau interfaciale, complexes enzymatiques...) mais au sens
d'une fonction qui repose sur une dynamique capable d'engendrer
des formes stables en son voisinage (synthèse
d'une chaîne polypeptidique, polymérisation d'un
microtubule, duplication d'un organite...).
« une enzyme est
entièrement définie par le réseau
d'interactions auxquelles elle participe ». (
en remplaçant "particule" par "enzyme", SSM, p 464)
Les formes des protéines se limitent
à un nombre limité de formes de base (ou
motifs) qui sont obtenus pour des séquences très
différentes. On peut interpréter ce fait d'une
part en considérant les profondes similitudes des aa
vis-à-vis du composant majoritaire de la cellule:
l'eau. Mais aussi en considérant que les formes
dynamiques "génératives" - dont les enzymes sont
la trace - existent en nombre limitées (tableau
ci-dessus).
De nombreuses protéines semblent
"déstructurées", c'est-à-dire
présenter une activité malgré une forme
très variable (LR, juin 2005). Ces protéines
peuvent être la trace d'innombrables dynamiques, plus ou
moins stables (beaucoup moins résistantes que les
dynamiques enzymatiques).
|
|
Un phénomène
représenté par une fonction
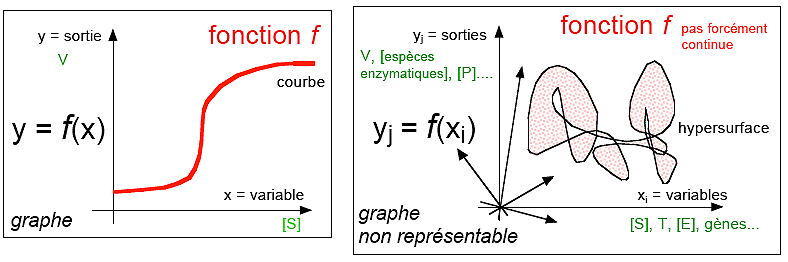
|
Remarque
Réintroduire
le continu en biologie
|
|
|
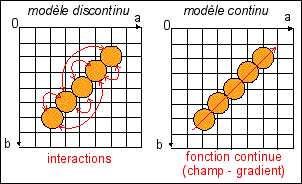
http://pst.chez.tiscali.fr/CT/continud.htm
Une illustration d'une interprétation des relations
entre des unités (des cellules, des molécules, des
individus... en
orange), situés dans un
plan (a,b) expérimental de contrôle
(a et b sont des paramètres mesurables; les unités sont
repérées par leurs coordonnées dans le plan de
contrôle), par un modèle discontinu
de réseau d'interactions
(flèches
rouges) versus un
modèle continu d'une fonction
sous-jacente relié par exemple à un champ de vecteurs
déterminant un gradient orienté dans le sens de la
flèche.
|
La fonction vivante (globale,
inaccessible) reste cachée;
le phénomène est supposé être
associé à une application
différentiable (locale, accessible).
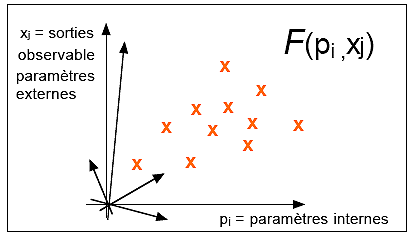
|
l'espace Rn
x RN
représente le métabolisme
(de métabolé =
changement)
|
|
1 ≤ i ≤ n
1 ≤ j ≤ N
|
|
Dans le cas d'un espace avec n ≤ 4 et N ≤ 2
René Thom a prouvé, par des calculs
non accessibles à des non
mathématiciens (c'est la notion de
déploiement universel d'une
singularité différentiable), qu'il
existe 7 catastrophes élémentaires et
seulement 7 (déjà vues dans la partie
2).
|
|
stabilité
de la fonction globale
|
=
|
homéostase
|
homéostase = état
d'équilibre intérieur d'un organisme
face à des modifications du milieu
extérieur.
homo = homœo
(latin), homolos (grec) = semblable - W. B.
Cannon (1932) homœo + stasie (=
position).
|
|
stabilité
de la fonction locale
|
=
|
points stables
de l'espace du métabolisme où la
dérivée de la fonction s'annule
(minima stables de potentiel)
|
=
|
singularités
de l'application F
|
=
|
points
catastrophe
|
|
|
La glycémie: un paramètre de
nombreuses fonctions de nutrition
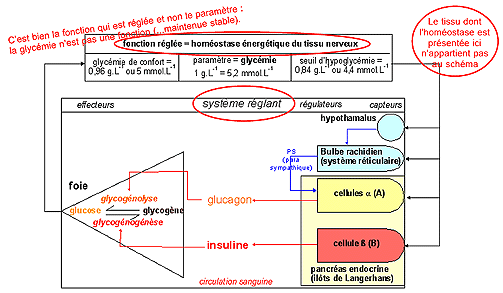
Schéma de régulation
classique issu de la cybernétique (science des
échanges d'information)
------------> Rechercher la fonction locale
|
|
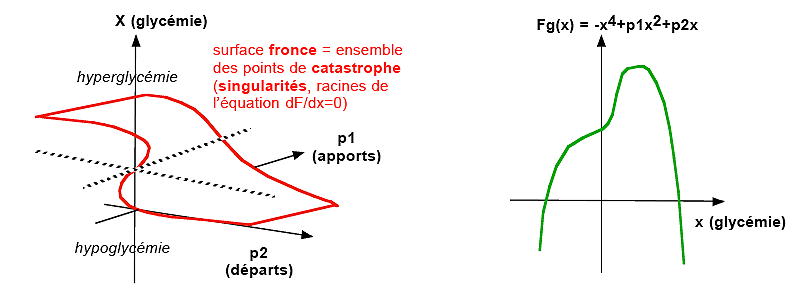
Modèle
catastrophique de l'homéostase glycémique
(catastrophe-singularité fronce)
F(p1, p2, x) = x4
+ p1x2 + p2 x
*
fonction locale = fonction de nutrition glycémique
(absorption, stockage,
déstockage, consommation...) ou fonction circulatoire
(au sens de flux qui permet de faire tourner une roue, ici
c'est le flux nutritionnel de glucose qui permet le
métabolisme glucidique des cellules).
* p1 = flux
entrant dans la circulation = apports en glucose (relatifs
à un apport moyen pour p1 = 0) par
alimentation-digestion-absorption ou réabsorption
rénale ou par libération (glycogénolyse
ou néoglucogénèse)
* p2 = flux
sortant de la circulation = départ de glucose (relative
à une consommation de base pour p2 = 0) par captation
par les cellules ou filtration rénale
|
|
--------------> Préciser les paramètres

|
|
Conclusion
* la sincérité
de l'enseignant favorise la vocation de chercheur du
lycéen.
* la biologie
théorique vaut la peine que l'on se donnera à
l'enseigner; elle est tellement neuve que les
élèves peuvent se passionner.
* il faut faire comprendre
à nos hommes politiques la nécessité
des mathématiques pour la biologie et se rebeller
contre l'idéologie démathématisante
actuelle.
|
L'enseignant n'est qu'une caisse de
résonance du travail de vulgarisation réalisé
par les chercheurs qui sont les seuls à pouvoir vulgariser
leur travail.
Son travail se rapproche sans aucun doute de celui du journaliste qui
ne peut se contenter au bout d'un temps d'être l'écho
des idées des autres.
Dans un articlede 2004 intitulé
"RÉFLEXIONS SUR LA PLACE DES MATHÉMATIQUES DANS
L'ENSEIGNEMENT SCIENTIFIQUE", Daniel
Duverney, Professeur de
Mathématiques Spéciales ATS (classe préparatoire
aux écoles d'ingénieurs réservée aux
titulaires de BTS et de DUT industriels), H.D.R. Membre du Conseil
d'Administration de la S.M.F., dénonce, chiffres et graphiques
à l'appui, une démathématisation de
l'enseignement scientifique au lycée. Ce renoncement aux
mathématiques est basé sur une nouvelle
idéologie que l'on pourrait résumer ainsi : ce
sont les sciences expérimentales, qui réalisent l'
unité de la science. Pour moi c'est un abandon de
certitude (de la raison), dans la mouvance relativiste. « Les
mathématiques sont trop sûres d'elles, or on est
sûr de rien, donc faisons moins de mathématiques
». Mon trajet est inverse. Les SVT que j'enseigne (que l'on
souhaite me voir enseigner) sont de plus en plus fausses et
relativistes, or j'ai besoin de certitudes, je me tourne donc vers
les maths.
À ceux qui s'inquiètent, et
ils sont nombreux parmi nos élèves à avoir des
difficultés en mathématiques au niveau de la
première S, il faut affirmer qu'il y a de la place pour
plusieurs filières biologiques: environnement, applications
biotechnologiques, santé, nutrition... Mais il est vain de
croire que la
recherche en biologie va pouvoir
longtemps se satisfaire du ridicule niveau de formalisation et de
mathématisation où elle s'est
cantonnée.
Pour éviter une catastrophe
annoncée au niveau de la recherche (et pas seulement en
biologie) il est urgent de redonner confiance aux
élèves en leur donnant des bases mathématiques
solides. Les mathématiques ne sont pas un luxe mais une
nécessité pour les scientifiques.