Statistiques... ou probabilités ?

accueil, panorama

Le mot «statistique» désigne à la fois un ensemble de données d'observation (c'est le «budget des choses» de Napoléon) et l'activité qui consiste dans leur recueil, leur traitement et leur interprétation (qui est la recherche d'une loi, souvent formalisée par des probabilités: on parle de théorie de l'inférence)(in Encyclopedia Universalis).

Quelle est la signification concrète d'une probabilité ?

• Du point de vue du phénomène observé que l'on cherche à modéliser au moyen de l'outil statistique on peut distinguer deux approches:
  • La loi de probabilité est une loi qui est la cause expérimentale du phénomène répétitif observé (modèle interne)
  • ou au contraire la loi de probabilité n'est que la simple formalisation de la répartition de comportements dont les causes sont à rechercher ailleurs (modèle externe).
• De même, du point de vue de l'observateur qui formule cette loi de probabilité, on distingue aussi deux approches que l'on qualifie d'objectiviste et de subjectiviste.
  • Les objectivistes, ou fréquentistes, considèrent que la probabilité fournit un modèle idéalisé du comportement des fréquences avec lesquelles peuvent se produire certains résultats d'expériences effectuées dans des conditions suffisamment stables.
  • Les subjectivistes pensent que la probabilité est une mesure du degré de confiance que nous pouvons avoir vis-à-vis de tout événement incertain; ce qui englobe le cas de la fréquence, mais aussi bien d'autres situations.

Cette page a été écrite en 2002 dans le but de réagir à l'article ci-contre. Voici quelques réponses qui m'ont été fournies dans plusieurs discussions avec des personnes plus compétentes que moi.

Plan

• 1. Formalisation mathématique (préambule)
• 2. Les statistiques en médecine: intuition et calculs
  • a. dépistage d'une maladie à l'aide d'un test
  • b. calcul d'un risque à partir d'un prévalence dans la population "générale"
  • c. utilisation de l'ADN en criminologie
  • d. une extension sur les diagnostics génétiques
  • e. conclusions

Annexe: épidémiologie

Soit une maladie que l'on s'efforce de détecter, à l'aide d'un test, dans un population donnée.

Quelques définitions épidémiologiques sont disponibles en annexe.

En statistique on s'intéresse à des événements :

probabilité des événements précédents :

p(M) = probabilité d'être malade = prévalence ou morbidité (voir annexe)

p(TP) = probabilité que le test soit positif

calculs grâce à l'axiome de Bayes:

La probabilité de l'occurrence simultanée des événements TP et M, soit (TP^M), est égale au produit de la probabilité de l'événement TP et de celle de l'événement M si TP à lieu, soit (M/TP) ou au produit de la probabilité de l'événement M et de celle de l'événement TP si M à lieu (TP/M)

p(TP^M) désigne la probabilité que le test soit positif et que la personne soit malade (intersection des deux événements ou occurrence simultanée de ces deux événements). La population de référence est ici l'ensemble de tous les individus, malades ou non, testés ou non (voir ci-dessous).

p(TP/M) désigne la probabilité que le test soit positif sachant que la personne est malade (probabilité conditionnée par l'occurrence de l'événement malade). La population de référence est ici l'ensemble des malades (voir ci-dessous). C'est en quelque sorte la sensibilité du test. Mais ce chiffre seul ne permet pas d'évaluer l'efficacité du test.

p(TP/NM) est le taux de faux positifs: probabilité que le test soit positif sachant que la personne est saine. Le taux de faux négatifs est p(TN/M) = 1- p(TP/M)

d'après la formule de Bayes :

Donc, du point de vue opérationnel, pour définir l'efficacité d'un test dans une population, on dispose habituellement de la proportion de malades p(M) (prévalence ou morbidité, selon les cas, voir annexe).

Mais, pour déterminer p(TP^M), qui est le chiffre habituellement recherché pour chiffrer l'efficacité du test, il est nécessaire de connaître la sensibilité du test p(TP/M) [ou le nombre de faux négatifs, soit p(TN/M) qui permet facilement de retrouver la sensibilité du test car p(TN/M) = 1- p(TP/M) ] ET le nombre de faux positifs : p(TP/NM). Ce qui fait bien un total de 3 données toujours nécessaires.

Une ou deux hypothèses...

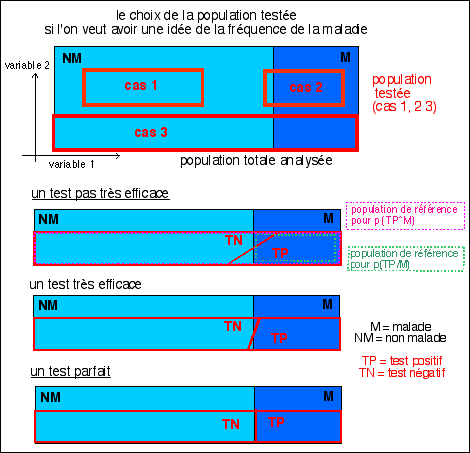
Comme dans toute analyse de fréquence réelle au sein d'une population de très grande taille une première hypothèse est que les fréquences au sein de la population testée sont les mêmes qu'au sein de la population totale. Le premier schéma ci-dessous est une illustration de cette hypothèse (qui n'est valable que dans le cas 3 seulement).

Un test qui englobe toute la population est aussi irréalisable, c'est donc une petite partie de la population qui est testée et donc les pourcentages obtenus de populations à test positif et à test négatifs n'ont pas la même signification... si le choix de la population à tester se fait par exemple en essayant de couvrir tout le champ de la variable 1 (cas 3), le test est significatif de la fréquence de la maladie dans la population; à l'inverse, si le choix de la population à tester se fait selon la variable 2 mais sans essayer de couvrir le champ de la variable 1 (cas 1 et 2), la population testée ne représente pas l'ensemble de la population pour la maladie.

2. Les statistiques en médecine: intuition et calculs

a. dépistage d'une maladie à l'aide d'un test

Un petit test a été proposé à des étudiants et des enseignants de la faculté de Harvard:

«Étant donné une maladie dont la prévalence (nombre de cas dans une population déterminée, sans distinction entre les cas nouveaux et les cas anciens) est de 1/1000 et pour laquelle il existe un test de dépistage donnant 5% de faux positifs, quel est le risque qu'une personne dont le test est positif soit effectivement malade (on ne sait rien d'autre de cette personne)».

Le résultat indiqué dans l'article est 2%. Le calcul proposé est de diviser le nombre de malades par la somme de ce nombre avec le nombre de faux positifs, soit 1/1000 divisé par 5% soit 2%.

analyse

Il manque une donnée (voir ci-dessus): la sensibilité du test (ou le nombre de faux négatifs).

Si l'on utilise le formalisme présenté ci-dessus, on peut poser les équations suivantes:
on recherche p(M/TP), on connaît p(M)= 0,1% et p(TP/NM)=5%
d'après la formule de Bayes p(M/TP)=p(M^TP)/p(TP), or p(TP)=p(TP/M)p(M)+p(TP/NM)p(NM) avec p(NM)=1-p(M) soit p(TP)=p(M)(p(TP/M)-p(TP/NM))+p(TP/NM)
toujours d'après la formule de Bayes, on a p(M^TP)=p(M)p(TP/M)
d'où p(M/TP)=p(M)p(TP/M)/p(M)(p(TP/M)-p(TP/NM))+p(TP/NM=p(TP/M)/(p(TP/M)-p(TP/NM))+p(TP/NM)/p(M)= 1/(1-p(TP/NM)/p(TP/M))+p(TP/NM)/p(M)

Les auteurs proposent p(M/TP)=1/(1+p(TP/NM)/p(M)) et négligent donc p(TP/NM)/p(TP/M) devant 1 (ce qui revient à dire que le test est extrêmement sensible: il n'y a quasiment pas de faux négatifs) et surtout devant p(TP/NM)/p(M) (ce qui revient à négliger les malades dont le test est positif par rapport aux malades...

Le deuxième exemple fourni dans le même article de La Recherche concerne la probabilité d'un cancer colorectal.

Le taux de base du cancer colorectal dans la population générale est de 0,3%. Le test hémocult a une sensibilité de 50% (un malade n'est détecté qu'avec une probabilité de 1 chance sur 2). Enfin le nombre de faux positifs est estimé à 3% (nombre de personnes n'ayant pas de cancer colorectal mais détecté comme malades par le test). La question est de calculer la probabilité qu'une personne, dont le résultat au test d'hémocult est positif, ait réellement un cancer colorectal.

Le résultat donné dans l'article est de 15 sur 315 soit environ 5%.
L'article montre que les médecins à qui ce test de calcul de probabilité à été présenté uniquement à l'aide de pourcentages ont échoué (1 sur 24 a réussi) alors que 16 sur 24 ont réussi lorsque le problème leur a été présenté avec des fréquences absolues avec le raisonnement suivant: sur 10.000 personnes, 30 ont probablement un cancer colorectal; sur ces 30, 15 auront un test hémocult positif; sur les 9970 personnes saines, 300 auront néanmoins un test positif.

analyse

Je ne conteste pas le côté pédagogique de l'article en ce qui concerne l'utilisation des fréquences absolues par rapport aux pourcentages , bien au contraire, c'est ce qui m'a séduit dans l'article, mais je souhaite montrer aussi le côté approximatif de ces calculs.

Cette fois les 3 données nécessaires au calcul sont présentes.
- p(M)=0,003
- la sensibilité du test reflète p(TP/M) qui est égale à 0,5
- p(TP/NM)=0,03

On obtient alors p(M/TP)=p(M^TP)/p(TP), or p(TP)=p(TP/M)p(M)+p(TP/NM)p(NM) avec p(NM)=1-p(M) et p(M^TP)=p(M)p(TP/M)
d'où p(M/TP)= p(M)p(TP/M)/(p(TP/M)p(M)+p(TP/NM)(1-p(M))
soit 0,003.0,5/(0,5.0,003 + 0,03. (1-0,003))= 5%

Mais il me semble qu'apparaît bien ici le problème des populations de référence qui ne sont pas les mêmes pour les chiffres présentés:
* la prévalence fait référence à une population statistique choisie dont on a étendue la fréquence à la population mondiale;
* la sensibilité du test fait référence à la population des individus testés.
Pour que le raisonnement proposé soit exact, il faut que TOUS LES MALADES SOIENT TESTÉS, ce qui n'est pas dit dans l'énoncé (et est impossible) puis TOUTES LES PERSONNES SAINES SOIENT TESTÉES, ce qui est encore moins possible.

Le troisième exemple est tiré des statistiques sur le sida expliqués par des conseillers médicaux (médecins) allemands.

Quel est le risque qu'un homme dont le test de dépistage au VIH est positif a d'être réellement contaminé ?
La prévalence (hétérosexuels allemands ne faisant partie d'aucun groupe à risques connu) est de 0,01%. Le test sanguin de dépistage du VIH produit environ 0,01% de faux positifs. Le risque qu'un homme dont le test de dépistage est positif a d'être réellement contaminé est donc de 50%. (1 malade sur 10.000 personnes; 1 faux positif sur 10.000; donc autant de chance d'être faux positif que malade: donc 50% de risque d'être réellement contaminé si le test est positif ).

Les données de cet exemple sont aussi incomplètes puisque l'on a pas la sensibilité du test.

Sinon le calcul est particulièrement démonstratif du côté non intuitif de la formule de Bayes et donc du résultat.

L'utilisation de l'ADN comme "preuve" dans le cas de procès (ici à la suite d'un viol) a aussi été testée auprès de juristes (étudiants et jeunes juges).

On considère que la probabilité que deux individus aient le même profil d'ADN est de 1/1.000.000 et donc on estime légitime de dire que la sensibilité du test est de 100% (en fait 99,9999 %). La fréquence des erreurs humaines (faux positifs) est de l'ordre de 3 pour 1000. Quelle est la probabilité pour que l'ADN retrouvé sur les lieux d'un crime soit bien celui de l'accusé si les profils sont identiques ? (Seuls 13% des juges et 1% des étudiants sont capables de trouver le bon résultat si le problème est posé en termes de probabilités alors que 68 et 44% des ces groupes ont trouvé le bon résultat lorsque le problème a été soumis en termes de fréquences absolue).

Le résultat attendu n'est pas indiqué dans l'article.

Il semble que le résultat attendu par les auteurs de l'article soit obtenu par un raisonnement similaire aux précédents du genre:
sur une population de 1000 suspects, 1 est coupable (et c'est là toute la difficulté du raisonnement car quelque soit la dimension de la population testée on considère qu'il y a un et un seul coupable) et 3 sont faux positifs (ADN identique et pourtant non coupables) et donc 3 sur 4 des réputés coupables sont innocents. La probabilité pour que l'ADN retrouvé sur les lieux d'un crime soit bien celui de l'accusé si deux profils sont identiques sur 1000 tests est donc de 25%, une chance sur 4....!!!!... et si le coupable n'est pas dans la population testée la probabilité devient bien sûr 0%.

Le fait de réduire la population d'individus testés ne change pas cette proportion de faux positifs qui est liée à la méthode. Par contre cela change la probabilité d'avoir un coupable si l'on considère toujours que le coupable DOIT être parmi les individus testés; sur 10,00 tests avec un coupable le nombre de faux positifs est de 0,03 et donc on a une probabilité d'erreur de 1-1/1,03 soit 3% (ce qui ne veut rien dire); sur 2,000 tests le nombre de faux positif devient 0,006 et donc celle d'une erreur est de 0,6% (1-1/1,006); enfin, si l'on ne fait qu'un seul test d'ADN sur un seul individu et qu'on ne suppose qu'un coupable, à quoi sert le test ? Il est donc clair, pour moi, qu'il n'est pas légitime de parler ici de probabilité. La probabilité s'efface devant la conviction d'avoir un coupable parmi les individus testés. Il reste aussi à se renseigner pour savoir si la proportion de faux positifs est exacte... personnellement elle ne me choque pas car je connais les risques que l'on prend à se tromper d'ADN quand on multiplie par PCR une molécule aussi omniprésente...

Pour les élèves du secondaire il est fréquent que des statistiques soient employées pour justifier de techniques de diagnostics avant avortement ou lors de "conseils génétiques". Il est essentiel de bien faire comprendre aux élèves que l'on manie ici des statistiques (modèle externe, sans recherche de causalité) et non une probabilité liée à un mécanisme biologique (modèle interne, avec une causalité supposée), même si le lien existe certainement entre eux.

Par exemple le risque d'avortement provoqué par l'amniocentèse est estimé à 0,5% en France, et comme le risque trisomique estimé atteint cette valeur de 0,5% seulement à partir de 38 ans, c'est à partir de cet âge seulement que la sécurité sociale prend en charge financièrement cet acte de diagnostic prénatal en France, à l'inverse des autres pays européens pour lesquels l'âge de prise en charge est de 35 ans.

Tout d'abord, le chiffre des amniocentèses "provoquant" une "fausse-couche" est une statistique expérimentale en quelque sorte liée à un geste "chirurgical" comportant des risques. Alors que celle portant sur le risque trisomique est une statistique dépendant de facteurs beaucoup plus sociologiques et économiques.
Ensuite, est-ce bien la même population de référence ? Non. D'un côté les femmes chez qui on pratique une amniocentèse -qui jusqu'à quelques dix ans était un geste rare, donc pouvant difficilement être objet de statistiques-, chacune avec un terrain personnel, un risque "opératoire" particulier, sans compter l'habileté du chirurgien et les conditions d'hygiène de l'hôpital... bref, nous ne sommes pas dans de le domaine de la science expérimentale théorique. Et de l'autre côté, des femmes enceintes de plus de 38 ans, chez qui le risque n'est pas du tout homogène (puisqu'il y a une nette augmentation de la fréquence des naissances d'enfants trisomiques de façon encore plus forte après 40 ans), et pour lesquelles la causalité biologique est fort discutée (voir cours de spécialité (Ch 1.3) pour quelques questions à ce sujet).
Je crois cependant comprendre que, en se basant sur ces chiffres -peut-être contestables par ailleurs-, pour chaque enfant trisomique détecté par amniocentèse, et (souvent) tué par avortement (50% ? je ne suis pas du tout sûr du chiffre, mais il est moins fort que l'on pourrait le craindre), un autre enfant sain l'est aussi, du fait du diagnostic. Est-ce supportable ?

Un autre chiffre: celui des trisomies détectées sur les femmes enceintes âgées de plus de 38 ans, qui atteint 3% des amniocentèses conduites.

A quoi correspond, biologiquement, ce chiffre ? En quoi reflète-il le taux réel d'anomalies chromosomiques de type trisomie après 38 ans ? Quel est le pourcentage d'anomalies qui conduisent naturellement à un arrêt de grossesse ? Comment le mesurer ? Quel est le pourcentage de femmes qui acceptent l'amniocentèse qui leur est maintenant proposé ? Quelle est l'influence de l'augmentation de l'âge moyen des mères et surtout de l'âge du premier enfant ? Quel est le terrain biologique de ces "nouvelles mères" ? Ces statistiques portent uniquement sur des européennes ou des américaines, qu'en est-il pour des femmes d'autres pays ?

Comme j'ai essayé de le montrer pour les notes de différentes disciplines (voir faq), je voudrais insister sur le fait que ces différents indices statistiques sont des indices que l'on pourrait qualifier de socio-médicaux et qui somment parfois des grandeurs de différentes nature. Par exemple la prévalence d'une anomalie génétique n'a pas beaucoup de sens en dehors d'une certaine population "génétique" (elle dépend du taux de dépistage, de la létalité, des comportements...), alors que la sensibilité d'un test dépend plus de variations individuelles. Si l'on essaie de calculer une probabilité relative à un individu on utilise alors ces chiffres en considérant qu'ils reposent sur le même type de phénomènes, ce qui n'est qu'une forte approximation.

Dans le cas par exemple de la "preuve par l'ADN", le postulat de base est que toutes les cellules d'un individu possèdent le même profil d'ADN nucléaire, que cet ADN est entièrement extrait par la technique, que les enzymes de restriction le coupent toujours aux mêmes endroits, que la migration se fait toujours de façon proportionnelle à la taille des fragments et sans aucun mécanisme interférant (ou alors que ces mécanismes sont identiques pour tous les ADN et pour toutes les manipulations....)... bref toute une série de postulats que j'avais déjà essayé de soulever dans le cours de terminale S (technologie de l'ADN recombinant). Il ne faut pas clore le débat. La compréhension des statistiques par les juristes est une chose, les postulats de la méthode sont un autre problème. Ce qui est acceptable pour un scientifique qui cherche un modèle génétique (une vérité scientifique) ne l'est pas forcément pour un juge qui cherche une vérité morale.

On peut aussi regretter quelques confusions dans le texte de l'article et dans les figures. Le danger ne vient pas de l'usage des % en probabilité mais bien d'oublier de préciser LA POPULATION DE RÉFÉRENCE dans chaque cas, erreur qui ne me paraît pas évitée par les auteurs de l'article.

Quelques données d'épidémiologie (d'après Microbiologie, Prescott, Harley, Klein, De Boeck Université, 1995, p 699) qui feront sourire les spécialistes mais j'avoue être très incompétent dans ce domaine et je voudrais aider à une petite mise au point:

statistiques

Il est préférable de parler de taux parce que en plus de la fréquence il est important de préciser une durée.

Les fréquences sont exprimées en fractions mais on devrait pas simplifier les dénominateurs et numérateurs: au numérateur, le nombre d'individus atteints et au dénominateur, la population de référence ou encore population à risque ou encore le nombre d'individus où l'affection peut avoir lieu. La population de référence n'est PAS une population théorique mais une population définie.

Une maladie qui représente 15 cas sur une population à risque de 15.000 individus de sexe masculin habitant Paris et d'âge compris entre 20 et 45 ans, N'EST PAS équivalente à une probabilité de 1/1000 sans autre précision.

Le taux de morbidité mesure le nombre d'individus atteints d'une maladie spécifique au sein d'une population déterminée et au cours d'une période déterminée. C'est un taux d'incidence qui reflète le nombre de nouveaux cas au cours d'une période.

ex: 700 nouveaux cas de grippe dans une population de 100.000 individus en une année donne un taux de morbidité de 0,7%.

Le taux de prévalence mesure le nombre total d'individus affectés par une maladie à un moment donné sans tenir compte du début de la maladie. Il dépend donc fortement de la durée de la maladie et du taux d'incidence ou de morbidité.

ex: pour le SIDA parmi les recrues américaines entre 1985 et 1989 le taux de séroprévalence est de 1,42 pour 1.000 hommes (0,14%) et 0,66 pour 1.000 femmes (0,06%)

Le taux de mortalité est le rapport entre le nombre de décès attribués à une maladie donnée (agent causal unique) et le nombre total de cas de cette maladie; toujours pour une période donnée.

ex: sur 15.000 morts du SIDA en un an pour 30.000 séropositifs pendant cette même année, le taux de mortalité est de 1/2 ou 50%.

L'événement maladie s'estime à partir d'un certain nombre de tests (visuels, cliniques, physiologiques...) et est donc lui-même une donnée statistique. Lorsque l'on étudie la sensibilité d'un test, celle-ci se superpose à la sensibilité de la détection clinique de la maladie, fort difficile à évaluer.