nouvelle version 2011
	Les mathématiques sont un langage universel. Les scientifiques en ont besoin pour communiquer. Le fait que les chercheurs puissent tous se comprendre, grâce aux mathématiques, est un fondement du caractère scientifique de leur travail (au contraire de la magie... ou de la philosophie qui utilisent le langage ordinaire), bien davantage que l'expérience. Les SVT ont besoin des mathématiques comme outil universel de la science.		Les mathématiques doivent vous devenir familières.		Bien évidemment vous avez le droit de ne pas trop aimer les maths et souhaiter pourtant continuer des études de biologie. Il y a de la place pour tous: médecins, horticulteurs, agronomes, vétérinaires, métiers de l'environnement, de l'agro-alimentaire, du sport... Tous ces métiers demandent au moins des bases de biologie. Mais vous admettrez que si vous désirez vraiment comprendre la vie et faire de la recherche en biologie, il vous faut des outils universels et scientifiques. Pour la recherche les mathématiques sont indispensables*.
	La recherche biologique a besoin de jeunes esprits qui n'aient pas peur des maths.
	1. Tracer une courbe c'est faire l'hypothèse d'une fonction sous-jacente au phénomène observé
	Si l'on vous donne ou si vous obtenez par la mesure des points expérimentaux (et vous devez les avoir avec une incertitude), vous ne pouvez tracer une courbe qui corresponde au phénomène étudié que si vous supposez que le phénomène est représenté par cette courbe. En fait c'est un modèle que vous tracez. Un modèle plus ou moins fidèle. Le modèle met en relation les points expérimentaux. La relation c'est la fonction.		Une fonction c'est une application qui met en relation les éléments d'un espace de départ avec ceux d'un espace d'arrivée. Tracer un graphe c'est représenter la fonction dans un espace qui est le produit de l'espace "des entrées" (dit espace "de contrôle" ou "de départ") par l'espace "des sorties" (ou espace "des phénomènes", ou "des observables" ou encore "d'arrivée").		En lycée (même jusqu'en classe de terminale S) vous n'aurez qu'un espace à 2 dimensions (une entrée (x) - le paramètre; et une sortie (y) - la valeur de la fonction) et donc des courbes dans un PLAN, mais vous comprendrez bien que si l'on veut modéliser le vivant il faut s'attaquer à des espaces de bien plus grande dimension et même à un espace de dimension infinie. Je vous rappelle qu'en biologie les fonctions globales sont les fonctions de nutrition, de relation et de reproduction (voir cours de seconde). Elles ne sont pas simples et il est clair qu'il faut utiliser des espaces de grandes dimensions si on veut essayer de les approcher.
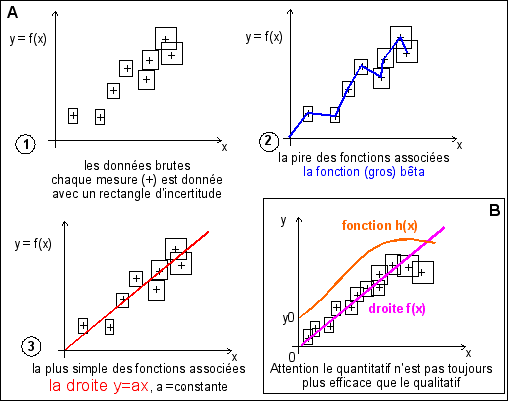
	Bien choisir sa fonction
	On choisit en SVT la fonction la plus SIMPLE possible et la plus RÉGULIÈRE possible. Mais, attention, le biologiste n'oublie pas qu'il essaye de modéliser le vivant et chaque fois que nécessaire il précise les simplifications faites. En assimilant une théorie à une fonction on pourrait dire avec René Thom (SSM, p 36) que la quantitatif n'est pas toujours plus efficace que le qualitatif. Par exemple (graphe B) si quantitativement (c'est-à-dire numériquement) la droite f(x) permet de passer au plus près des points expérimentaux, elle modélise très mal la fonction biologique représentée sur le graphe. La fonction h(x), quantitativement éloignée des points de mesure (car placée trop haut sur l'axe des y étant donné la valeur de y0) est peut-être une bien meilleure fonction (au sens qualitatif de théorie) pour modéliser le phénomène représenté.
	Deux fonctions usuelles en classe de seconde
	fonction constante		f(x) = a		a = constante la courbe est une droite horizontale d'ordonnée a
	fonction polynôme de degré 1		f(x) = ax + b		a et b sont des constantes la courbe est une droite de pente a (pour deux points (x1,y1) et (x2,y2) la pente est définie par (y2-y1)/ (x2-x1) = a) et d'ordonnée à l'origine b (si b=0, la droite passe par (0,0))
	complément pour les élèves de 1èreS et Terminale S
	2. Un peu de vocabulaire pour décrire une courbe (non exhaustif)
	Plus vous utiliserez un vocabulaire mathématique précis, mieux vous vous ferez comprendre.
	domaine de variation sens de variation proportions, intensité de la variation stabilité, régularité À UTILISER 1 - la fonction prend des valeurs de.... à .... - la variable (x) est comprise entre .... et ..... 1 - la fonction est croissante / décroissante entre.... et .... - on observe une variation positive / négative de y entre les valeurs .. et .... - pour deux valeurs successives de x, y augmente / diminue de .... 1 - la pente de la droite est positive / négative / nulle (courbe horizontale) - la pente est minimale / maximale entre..... et ... - la courbe varie très fortement (très rapidement si c'est le temps qui est en abscisses) .... - la courbe présente un maximum / minimum pour x = ...; 1 - la fonction varie régulièrement / irrégulièrement - la fonction est constante (stagne si le paramètre x est le temps) sur l'intervalle (x1... x2). À NE PAS UTILISER la courbe va de ... à .... - la courbe va en haut / en bas... - la courbe est plus grande... - la courbe est maximale /minimale la courbe monte et descend, bouge, se déplace, revient, repart... la courbe est continue / discontinue
	*Ne croyez pas que l'on vous demande en lycée plus de mathématiques qu'avant. Au contraire, il y a une incontestable démathisation (ou démathématisation) de l'enseignement secondaire; quelques références à ce sujet: - un article de 2004 de Daniel Duverney : "RÉFLEXIONS SUR LA PLACE DES MATHÉMATIQUES DANS L'ENSEIGNEMENT SCIENTIFIQUE"; l'auteur est Professeur de Mathématiques Spéciales en ATS (classe préparatoire aux écoles d'ingénieurs réservée aux titulaires de BTS et de DUT industriels), H.D.R. Membre du Conseil d'Administration de la S.M.F. - le rapport du Professeur Demailly: http://www-fourier.ujf-grenoble.fr /~demailly/ rapport.html - les pages du Professeur Laurent Lafforgue, académicien et médaillé Fields http://www.ihes.fr/% 7elafforgue/ education.html				Une page à conseiller : http://svt.ac-creteil.fr/spip.php?article1634
					retour
	concepts mathématiques fondamentaux pour les SVT Ce tableau ne présente que les notions générales qui me paraissent essentielles et non pas les outils mathématiques qui font partie de l'attirail ordinaire du scientifique.   programme 2009 maths classe 2nde		Première S Terminale S Analyse fonctions trinômes (f(x)=ax2+bx+c, a≠0) fonctions rationnelles opérations sur les fonctions dérivée en un point et fonction dérivée notion de continuité (en un point et sur un intervalle) dérivées et primitives (pour le calcul différentiel) équations différentielles (x'=ax+b) statistiques et probabilités statistiques (moyenne, variance, écart type, médiane, quartiles) définitions (événements et loi de probabilité) lois de probabilité usuelles algèbre trinômes et équations du second degré polynômes (définition, racines) géométrie vecteurs repères transformations dans le plan et dans l'espace (isométries de type translations, symétries axiales, rotations; homothéties)