ancienne version
	Les mathématiques sont un langage universel. Les scientifiques en ont besoin pour communiquer. Le fait que les chercheurs puissent tous se comprendre, grâce aux mathématiques, est un fondement du caractère scientifique de leur travail (au contraire de la magie... ou de la philosophie qui utilisent le langage ordinaire), bien davantage que l'expérience. Les SVT ont besoin des mathématiques comme outil universel de la science.		Les mathématiques doivent vous devenir familières. Cette fiche provient d'un double constat: - le niveau de mathématiques des élèves atteint des abysses tels que l'on ne peut plus utiliser en classe de seconde des graphiques sans y passer un temps démesuré. - avec l'utilisation de logiciels disparates et inadaptés, les élèves sont incapables de construire un graphe et de tracer À LA MAIN une simple courbe qui modélise un phénomène.		Bien évidemment, vous avez le droit de ne pas trop aimer les maths et souhaiter pourtant continuer des études de biologie. Il y a de la place pour tous: médecins, horticulteurs, agronomes, vétérinaires, métiers de l'environnement, de l'agroalimentaire, du sport... Tous ces métiers demandent au moins des bases de biologie. Mais vous admettrez que si vous désirez vraiment comprendre la vie et faire de la recherche en biologie, il vous faut des outils universels et scientifiques. Pour la recherche les mathématiques sont indispensables*. La recherche biologique a besoin de jeunes esprits qui n'aient pas peur des maths.
	Cette page fait appel à des notions d'analyse (fonctions) et de géométrie (représentation plane) toutes revues en classe de seconde en maths. (programme 2009 maths classe 2nde)
	1. Des données expérimentales à la représentation graphique
	Les données expérimentales sont des mesures; elles sont obtenues avec une incertitude. La plupart des logiciels de représentation graphique (tableur-grapheur) sont des logiciels financiers et vous ne pouvez pas représenter l'incertitude ni choisir le type de modèle de façon souple: il faut donc apprendre à TRACER SES COURBES À LA MAIN. Les logiciels de mathématiques (Geogebra par exemple ci-dessous) ne sont pas prévus pour des MESURES expérimentales et ne permettent pas d'utiliser les incertitudes, et encore moins une régression. Pour un mathématicien 1,000 et 1 c'est la même chose ! Mais PAS pour un scientifique (la précision de chaque chiffre correspond à une certaine précision de la mesure). Un des seuls logiciels d'EXAO qui soit vraiment scientifique est LoggerPro de la firme américaine Vernier.
	2. Tracer une courbe c'est faire l'hypothèse d'une fonction sous-jacente au phénomène observé
	Si l'on vous donne ou si vous obtenez par la mesure des points expérimentaux (et vous devez les avoir avec une incertitude), vous ne pouvez tracer une courbe qui corresponde au phénomène étudié que si vous supposez que le phénomène est représenté par cette courbe. En fait c'est un modèle que vous tracez. Un modèle plus ou moins fidèle. Le modèle met en relation les points expérimentaux. La relation c'est la fonction.		Une fonction c'est une application qui met en relation les éléments d'un espace de départ avec ceux d'un espace d'arrivée. Tracer un graphe c'est représenter la fonction dans un espace qui est le produit de l'espace "des entrées" (dit espace "de contrôle" ou "de départ") par l'espace "des sorties" (ou espace "des phénomènes", ou "des observables" ou encore "d'arrivée").		En lycée (même jusqu'en classe de terminale S) vous n'aurez qu'un espace à 2 dimensions ; soit une entrée (x) - le paramètre; et une sortie (y) - la valeur de la fonction. Attention ! pour le biologiste comme pour le physicien, x et y sont des grandeurs mesurables qui s'expriment avec une incertitude. On voit bien ici que les termes de "paramètre de la fonction" et "valeur de la fonction", propres aux mathématiques, sont UN MODÈLE de la relation qui est supposée exister entre les grandeurs physiques. En lycée donc, toutes les courbes sont représentées dans un PLAN, mais vous comprendrez bien que si l'on veut modéliser le vivant il faut s'attaquer à des espaces de bien plus grande dimension et même à un espace de dimension infinie. Je vous rappelle qu'en biologie les fonctions globales sont les fonctions de nutrition, de relation et de reproduction. Elles ne sont pas simples et il est clair qu'il faut utiliser des espaces de grandes dimensions si on veut essayer de les approcher.
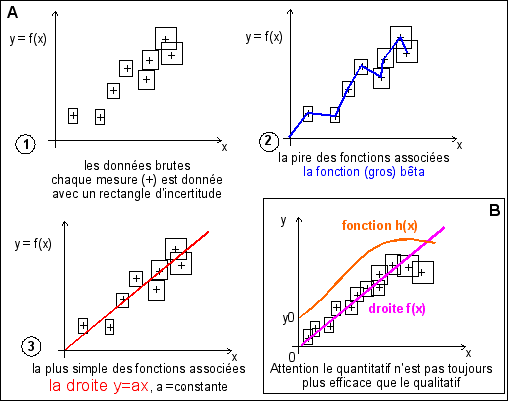
	Bien choisir sa fonction
	On choisit en SVT la fonction la plus SIMPLE possible et la plus RÉGULIÈRE possible. Mais, attention, le biologiste n'oublie pas qu'il essaye de modéliser le vivant et chaque fois que nécessaire il précise les simplifications faites. En assimilant une théorie à une fonction on pourrait dire avec René Thom (SSM, p 36) que la quantitatif n'est pas toujours plus efficace que le qualitatif. Par exemple (graphe B) si quantitativement (c'est-à-dire numériquement) la droite f(x) permet de passer au plus près des points expérimentaux, elle modélise très mal la fonction biologique représentée sur le graphe. La fonction h(x), quantitativement éloignée des points de mesure (car placée trop haut sur l'axe des y étant donné la valeur de y0) est peut-être une bien meilleure fonction (au sens qualitatif de théorie) pour modéliser le phénomène représenté.
	Le nouveau programme de la classe de seconde a multiplié les fonctions usuelles, mais en SVT, et en seconde, les deux premières SEULES sont essentielles.
	fonction constante f(x) = a a = constante la courbe est une droite horizontale d'ordonnée a fonction polynôme de degré 1 f(x) = ax + b a et b sont des constantes la courbe est une droite de pente a (pour deux points (x1,y1) et (x2,y2) la pente est définie par (y2-y1)/ (x2-x1) = a) et d'ordonnée à l'origine b (si b=0, la droite passe par (0,0))
	fonction inverse cas particulier des fonctions puissance) f(x) = x-1= 1 / x la courbe est une hyperbole fonctions polynomiales du second degré f(x) = ax2 + bx + c a, b et c sont des réels la représentation graphique est une parabole fonctions homographiques ax + b ______ h(x) = cx + d c ≠ 0 et a, b, c et d réels le graphe de la fonction est une hyperbole équilatère Un petit grapheur Java très commode
	Pour s'habituer au vocabulaire des fonctions périodiques: amplitude et période : j(x) = fa . sin (fp . x) : fonction périodique (de type sinusoïde) avec deux paramètres : fa = paramètre modifiant l'amplitude et fp modifiant la période
	3. Un peu de vocabulaire pour décrire une courbe (non exhaustif)
	Plus vous utiliserez un vocabulaire mathématique précis, mieux vous vous ferez comprendre.
			OUI (à utiliser)		NON (à ne pas utiliser)
	domaine de variation		- la fonction prend des valeurs de.... à .... - la variable (x) est comprise entre .... et .....		la courbe va de ... à ....
	sens de variation		- la fonction est croissante / décroissante entre.... et .... - on observe une variation positive / négative de y entre les valeurs .. et .... - pour deux valeurs successives de x, y augmente / diminue de ....		- la courbe va en haut / en bas... - la courbe est plus grande... - la courbe est maximale /minimale
	proportions, intensité de la variation		- la pente de la droite est positive / négative / nulle (courbe horizontale) - la pente est minimale / maximale entre..... et ... - la courbe varie très fortement (très rapidement si c'est le temps qui est en abscisses) .... - la courbe présente un maximum / minimum pour x = ...;		la courbe monte et descend, bouge, se déplace, revient, repart...
	stabilité, régularité		- la fonction varie régulièrement / irrégulièrement - la fonction est constante (stagne si le paramètre x est le temps) sur l'intervalle (x1... x2).		la courbe est continue / discontinue
	*Ne croyez pas que l'on vous demande en lycée plus de mathématiques qu'avant. Au contraire, il y a une incontestable démathisation (ou démathématisation) de l'enseignement secondaire; quelques références à ce sujet: - un article de 2004 de Daniel Duverney : "RÉFLEXIONS SUR LA PLACE DES MATHÉMATIQUES DANS L'ENSEIGNEMENT SCIENTIFIQUE"; l'auteur est Professeur de Mathématiques Spéciales en ATS (classe préparatoire aux écoles d'ingénieurs réservée aux titulaires de BTS et de DUT industriels), H.D.R. Membre du Conseil d'Administration de la S.M.F. - le rapport du Professeur Demailly: http://www-fourier.ujf-grenoble.fr /~demailly/ rapport.html - les pages du Professeur Laurent Lafforgue, académicien et médaillé Fields http://www.ihes.fr/% 7elafforgue/ education.html				Une page à conseiller : http://svt.ac-creteil.fr/spip.php?article1634
					retour