fonctions pour les SVT (1ère et terminale scientifiques)

Deux fonctions usuelles en classes de première ou terminale scientifiques

fonction puissance f(x) = x^m
^ou

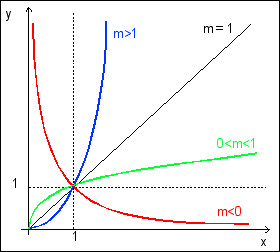
f(x) = e^mlnx

m≠0, m réel

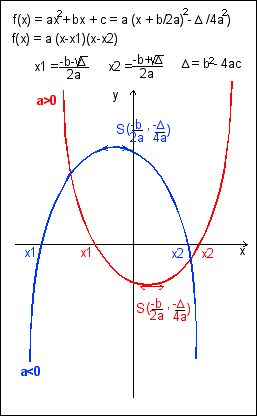
fonctions polynômiales du decond degré f(x) = ax² + bx + c
a, b et c sont des réels
la représentation graphique est une parabole

fonctions homographiques

ax + b
______

h(x) =

cx + d

c ≠ 0 et a, b, c et d réels

le graphe de la fonction est une hyperbole équilatère

fonction logarithme népérien
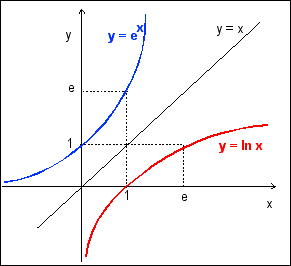
la fonction logarithme népérien, notée ln(x), est la primitive de la fonction g(x)=1/x définie de ]0;+∞[; elle s'annule pour x=1; elle réalise une bijection strictement croissante de ]0;+∞[ sur l'ensemble des réels
(ln)' (x) = 1/x
ln (ab) = ln a + ln b ; ln (a/b) = ln a - ln b ; ln (1/b) =- ln b ; ln (a^p) = p ln a

e^a+b = e^a e^b; e^-b = 1/ e^b ; e^a-b = e^a / e^b ; (e^a)^p = e^ap

fonction exponentielle
la fonction exponentielle est la bijection réciproque de la fonction logarithme népérien; elle est strictement croissante sur ]0;+∞[
exp (x) = e^x