version corrigée

Objectif notionnel : la grandeur expérimentale "pression" en biologie et en géologie

Objectif méthodologique : unités de mesure d'une grandeur physique, conversion d'unités

version non corrigée (pdf)

La pression est une grandeur mesurable (expérimentale) qui représente la force qui s'exerce sur une surface.

Faites un petit schéma (crobard) représentant la notion de pression (force verticale perpendiculaire à la surface):

Les unités de pression sont très variables selon les moyens de MESURE. Dans le système d'unités international (SI) elle doit être exprimée en pascals (Pa). En effet le pascal correspond à une force de 1 newton (1 N) exercée sur une surface de 1 m² , soit 1 N.m^-2.

Remarque: le newton, unité de force, peut s'exprimer à l'aide d'unités plus SENSIBLES si l'on remarque par exemple que le poids est une force. Le poids est une masse (en kg) multipliée par l'accélération de la pesanteur (en m.s^-2). Dans le système international N = kg.m.s^-2.

Une unité tolérée est le millimètre de mercure (mm d'Hg) ou Torr (avec 1 Torr = 1 mm d'Hg = 133,3 Pa). La pression est alors mesurée à l'aide d'un tube de verre placé sur une cuve à mercure. Les atmosphères et le bar ne sont plus acceptés.

Relier les unités de pression entre elles sachant que :

La pression atmosphérique de nos laboratoires (1 atmosphère) à de faibles altitudes est d'environ 101,3 kPa ; 1 atm équivaut à 760 mm d'Hg dans les mêmes conditions; 1 bar est égal à 10⁵ Pa.

3.1 Citez quelques pressions usuelles en biologie-géologie:

géologie: pression hydrostatique, pression lithostatique
biologie : pression artérielle, pression osmotique, pression oncotique....

3.2 - Comment varie la pression atmosphérique ?

L'air a une masse volumique toujours décroissante vers le haut, ce qui revient à rejeter à l'infini la limite théorique de l'atmosphère. On est ainsi conduit à considérer que telle fraction de la masse totale de l'atmosphère se situe au-dessous de telle altitude. Par exemple, on peut affirmer qu'en moyenne la moitié de la masse de l'atmosphère se situe au-dessous de 5 500 m; les 2/3 au-dessous de 8 400 m; les 3/4 au-dessous de 10 300 m; les 9/10 au-dessous de 16 100 m; les 99/100 au-dessous de 31 000 m, etc. Les mesures faites à 200 km (8,5.10^-7 hPa) et 300 km (8,8.10^-8 hPa) correspondent au vide que l'on obtient en laboratoire.

3.23- Comment relier la profondeur avec la pression hydrostatique ?

La pression hydrostatique représente le poids de la colonne d'eau située au-dessus d'un point situé sous la surface. Cette valeur s'ajoute à la pression atmosphèrique (P_atm). On suppose la plupart du temps que la densité de l'eau (µ) est fixe et égale 1,03 g.cm^-3, ce qui est évidemment faux pour de l'eau naturelle dont la densité varie en fonction de la salinité (l'eau est d'autant plus dense qu'elle est salée) et de la température (l'eau est d'autant moins dense qu'elle est chaude).
En supposant une colonne cylindrique d'eau de section S (surface d'une section) et de hauteur H, la formule donnant cette pression est donc :

 comme le volume d'un cylindre est égal à la section S (en m²) multipliée par la hauteur H (en m), on a :

en simplifiant par S, on a :

Si l'on considère que µ ~= 10³ kg.m^-3 et que g est à peu près égal à 10 m.s^-2 , on peut alors considérer qu'il suffit de multiplier la profondeur (en m) par 10⁴ pour avoir la pression de la colonne d'eau en Pa (c'est à dire en N.m^-2).

D'où la formule approximative pratique :

Remplissez le tableau avec quelques valeurs caractéristiques :

P_atm = 1 atm ~= 10⁵ Pa

profondeur (m)	pression (N.m-2) = Patm + Ph	lieux
10	2.105	rivage
200	21.105	plateau continental
2000	201.105	sommet d'une dorsale
4000	401.105	plaine abyssale
12000	1201.105 = 0,12 GPa	fosse abyssale

3.3 - Comment relier la profondeur avec la pression lithostatique ?

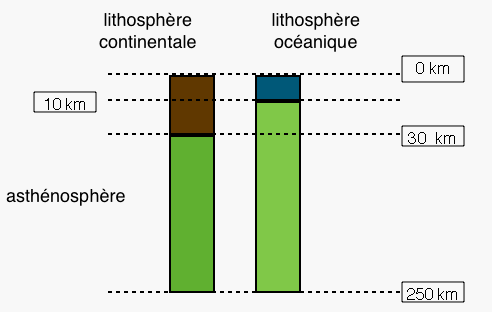
Dans les diagrammes P, T il est fréquent d'utiliser la distance (en km) à la place de la pression; le diagramme P, T est donc en fait un diagramme profondeur = f (température).

La pression lithostatique est la pression exercée par la colonne de "terre" placée au-dessus d'un point du sous-sol. Elle dépend donc de la densité des roches de cette colonne. Comme l'on connaît la densité MOYENNE des roches de la lithosphère : 2,7 pour une croûte continentale, 2,9 pour une croûte océanique et 3,3 pour le manteau lithosphérique (bien que l'asthénosphère ait une densité très variable, on supposera pour le calcul une densité moyenne de 3,4 ); on peut donc en déduire la relation entre la pression lithostatique P_l et la profondeur (p). On utilisera les mêmes unités que celles utilisées pour la pression hydrostatique : attention, il est fortement conseillé de tout convertir dans le SI d'unités.

P_l = p.µ.g avec p en m, µ en kg.m^-3 (µ = d.µ_eau) et g en m.s^-2

P_l à la base de la lithosphère continentale = 30.000 . 2,7 10³.10 Pa = 8,1 10⁸ Pa = 0,81 Gpa

P_l à la base de la lithosphère océanique = 10.000 . 2,9 10³ . 10 Pa = 2,9 10⁸ Pa = 0,29 Gpa

P_l à la base de l'asthénosphère
--sous un continent : 220.000 . 3,3 10³ .10 + 8,1 10⁸ Pa = 80,7 10⁸ Pa = 8,07 Gpa
- sous un océan : 240.000 . 3,3 10³ .10 + 2,9 10⁸ Pa = 82,1 10⁸ Pa = 8,21 Gpa

3.45- Comment PERCEVOIR de très grandes pressions ?

La pression lithostatique à la base de l'asthénosphère est très élevée et le chiffre exprimé en newton ne permet pas forcément de PERCEVOIR (sentir) sa valeur. Pour s'approcher de cette perception, on peut utiliser d'anciennes unités qui facilitent les analogies.

Le kilogramme-force (kgf) est égal à 9,807 N.m^-2 (soit 9,807 Pa) est la pression exercée par un poids d'un kg sur une surface d'un m². On notera que la pression à la limite manteau-noyau est estimée à 135 GPa.

Remplissez le tableau suivant :

analogie	pression en kgf	pression en (N.m-2) ou Pa	pression en atm (1 atm ‰ 105 Pa)
camion de 10 tonnes (105 kg) reposant sur une surface d'1 m2	105	106 Pa = 1 MPa	10
le même camion de 10 tonnes reposant sur une surface 1 mm2	1011	1012 Pa = 1000 GPa = 1 TPa	107
presse d'une cellule à enclume de diamant développant une force de 3 kg sur une surface de 100 µm2 (10 µm x 10 µm)	3.1010	3.1010 Pa = 300 GPa	3.106

3.6 - Que représente la preSsion dans un vaisseau ?

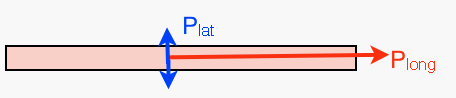
 La pression d'un liquide dans un tube n'est pas définie par une seule grandeur. Combien de grandeurs doit-on au minimum considérer si le tube est assimilé à un tube RIGIDE de DIAMÈTRE CONSTANT ? Les représenter sur ce petit schéma :

Au moins deux grandeurs: la pression latérale (P_lat) exercée par les parois du tube (constante puisque le tube est rigide) et la pression longitudinale (P_long) somme de celles exercées par le liquide en amont (pression de sortie du cœur et gravitaire...)et en aval (résistance périphérique...).

La pression au niveau des artères est très sensible au fonctionnement de la pompe cardiaque puisque les artères sont les vaisseaux où circule le sang venant directement du cœur. On donne donc habituellement trois valeurs à la pression artérielle:

- la pression maximale ou systolique (p_s) qui correspond à l'éjection du sang par le cœur qui se contracte (phase de systole)
- la pression minimale ou diastolique (p_d) qui correspond au relâchement et au remplissage du cœur (phase de systole)
- la pression moyenne (pa_m) qui tient compte de la durée moyenne des deux phases : p_am = p_ad + 0,333 (p_as-p_ad).

Calculez dans le SI la p_am d'un sujet dont les pressions systolique et diastolique sont de 120 et 80 mm d'Hg. 93 mm d'Hg = 93. x133,3 Pa = 0,12397.10⁵ Pa